基于量子纠缠弱测量的超光速通信方案探究

　　王 楠（西安科技大学，西安 710054）

　　摘 要：由于量子信道的纠缠特性在量子通信方面没有很好的发挥，本文提出了一种测量量子信息改变量的量子通信方式，该方法能够绕过量子通信中的经典信道部分，并借助弱测量的方法使得其在试验中有极大可能可以实现，从而实现超光速通信。

　　关键词：量子纠缠；弱测量；通信

　　0 引言

　　随着量子力学的发展，量子纠缠特性越来越成为量子信息领域中不可替代的重要资源，它己被广泛应用于量子通讯、量子密钥分发和量子隐形传态等各种量子处理过程中 ^[1-2] 。量子纠缠体现出的多个量子系统之间存在非经典的特点，例如强关联性和非定域性，是能够区别量子领域和经典领域的一个显著特征。由于纠缠态具有强关联的特点，因此两个粒子无论在空间距离上有多远,它们互相之间都会有量子领域的联系，如果对其中一个粒子的测量将会使另外一个粒子量子态的状态出现塌缩 ^[3] ，即能够确定粒子的状态。对于这种鬼魅般的超距作用，在量子远程通信中是很有发展前景的。

　　1 基本原理

　　在量子力学理论中，人们习惯上将半自旋粒子A和B (EPR对)的两个态分别记为|0>和|1>，|0>表示粒子自旋方向向上，|1>表示粒子自旋方向向下。它们作为一个系统处于如下的量子态(称为EPR 态) ^[4] :

　　|Ψ (A, B)>= (|0> A |1> A - |1> A |0> B ) (1)

　　这就是粒子之间的一种量子纠缠态。对其所表示的量子态系统在被测量之前，每一个粒子的自旋状态虽然只有两种，但都是不确定的，只能单独地计算出其中一个粒子被测量后得到的一种结果的概率是1/2，一旦某个人测量了其中一个粒子的自旋状态，那么另外一个粒子的自旋状态也就立刻确定下来，即为前一个粒子相反的状态；而且不论两个粒子在空间上相距多远，只要这种纠缠特性不消失，它们都处于这种相互关联的状态，这就是量子力学的非局域效应(non-local effect)。

　　如今根据文献^[1]在量子通信中使用的技术是量子隐形传态，可以从其基本原理中找到进行远程通信的方法。然而量子隐形传态需要经典信道，这一部分却制约了量子纠缠在通信中的先天优势。如果能够克服经典通信的限制，那么会对量子通信带来极大的发展。但我们如何才能看到“盒子里的猫”呢？

　　2 利用弱测量进行量子通信的设想

　　由于在上述量子隐形传态中，需要传送的是未知态粒子的全部量子信息，就只能通过提取量子信息和经典信息的方式来传送。这对于量子保密通信是很有用的，但不能解决远距离通信。经典信道的延迟和干扰，以及对传统网络的负载压力对于追求安全准确大容量的通信方式来说无疑是短板一块。因此，如何绕过经典信道来传输信息就是本文研究的主要问题。

　　而由于量子态的塌缩效应，无论测量或是观察均会引起量子态的塌缩，使其失去量子态的各种属性，从而产生退相干。为了避免塌缩，我们可以使用弱测量的方法，量子弱测量实质是在冯·诺依曼测量和半正定算子值测量的基础上发展出来的一种部分塌缩测量。在两比特量子态遭遇退相干环境之前执行前置的量子弱测量并在遭受环境后执行相对应的反馈测量能有效地保护量子态的纠缠 ^[5] 。从原理机制上看，结合前置的量子弱测量和后置的反转测量能有效地抑制退相干的原因主要有两点：第1，执行前置量子弱测量的作用是先降低系统激发数所占的权重，以便在遭遇噪声环境时减少受其影响；第2，执行反转测量的作用是使量子态与噪声环境作用以后重新恢复激发数的权重，可以使被破坏的初始态得到概率性恢复。在量子弱测量的方案中，单次进行测量时不会出现波包塌缩的情况，并且可以保留量子系统的相干叠加性，其代价是进行一次测量得到的关于系统的信息量很小 ^[6-7] 。随后可以将小信号进行放大，直到能够检测到量子系统的改变量即可，这样就可以测得信息。

　　上文提到的弱测量已经在实验室中实现，R. Vijay领导的小组完成了名为《量子位的量子反馈控制》的弱观测实验报告 ^[8] ，这是一个基于频率的测量。其中设计的反馈控制环路能够产生反馈来修正系统观测所带来的影响，从而测量并记录了能够连续跟踪和使用反馈的量子态，能够使用超导回路在不破坏量子态的前提下进行量子测量，并且已经证明了：一个连续的模拟反馈方案能够稳定地在超导量子比特回路下进行振荡，并使他们独立持续地存在。

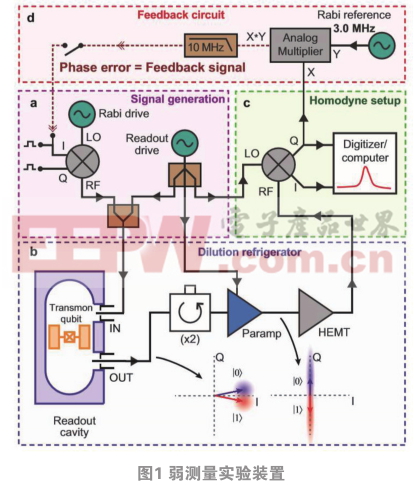
　　其具体的实验方法是：搭建一个量子系统，如图1，一种由一个电容并联的约瑟夫森结实现的非谐振荡器，弥散耦合于一个三维微波腔中。使用两个最低能级（ω01/2π=5.4853 GHz）形成一个量子比特。在基态的量子比特的谐振腔的谐振频率是ωc/2π=7.2756 GHz。强耦合的输出端口设置的谐振谱线宽度13.4 GHz，而控制和测量信号通过弱耦合输入端口注入。量子位腔耦合导致了在腔输出字段的一个状态依赖相移(0.687 GHz)，其中的状态信息包含在一个正交信号上。腔的输出发送到附近的一个无噪声的相位敏感的参量放大器（结）以促进相关正交电路到与经典电路相适应的水平。该参量放大器输出被进一步放大和零差检测，以使得扩增的正交（Q）包含了最终的测量信号。

　　在此思路上，提出了基于量子信息改变量的量子通信方式，即：可以从传送完整的量子态到只传送部分量子态，进而测量前一次传送和后一次传送的改变量即可。例如，若设第一次传送的状态为|0>，第二次传送的状态为|1>，则可判断为一次改变，记为1；若第二次仍为|0>，则记为0。由于量子态的纠缠性，在发送端进行一次前置弱测量，就会改变量子系统的状态。

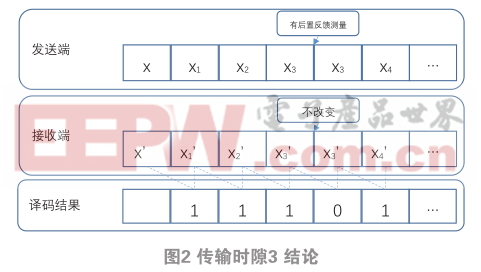
　　而具体的通信过程，可以分为通信部分和测量部分,它们是相互交织的。我们可以定义时隙T，初始状态设为未知量x，接受端先进行一次弱测量，记录下此时的状态x’，在T时间后发送端进行一次弱测量，此时只进行前置弱测量，即改变发送端量子态，接收端进行一次完整弱测量，记录下此时的状态x 1 ’，若在T时隙内在发送端不进行后置反馈测量，则x’一定与x 1 ’不同（此处可设定阈值），此T时隙即发送“1”；若在T时隙内在发送端进行后置反馈测量，则不改变量子态，即x’与x 1 ’相同，此T时隙即发送“0”,如图2。由于发送一位编码需要两个时隙，所以时隙不可间断，且由于码字只与此时隙和上一时隙有关，所以此系统抗干扰能力强。时隙的大小可以决定系统的传输速率，在同一个传输系统中，时隙应该设定为同一个数值。从而能够实现同步。若没有后置反馈测量回路，则最终会破坏纠缠关系，所以在0和1的编码设置上有待改进，从而延长系统纠缠有效时间。

　　3 结论

　　如果本文提出的量子通信方法行之有效，那么信息的超光速传输将会成为现实，将对信息技术行业乃至太空探索都有绝对的重要性。而就目前来说，本文所提的方法实现困难，造价高昂，因此还需进行理论完善和实验，且具体实现方法均有待改进。

　　参考文献

　　[1] Bennett C H，G Brassard，C Crepeau, et al. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels[J].Physical Review Letters,1993,70:1895.

　　[2] Nielsen M A. Quantum Computation and Quantum Information[M]. Cambridge University Press, Cambridge, England,2000.

　　[3] 葛华.量子安全直接通信及网络技术研究[D].湖北:华中科技大学,2014.

　　[4] 苏晓琴,郭光灿.量子隐形传态[J].物理学进展,2004,24(3).

　　[5] 何娟.量子弱测量及量子关联相关问题研究[D].安徽大学,2015.

　　[6] 玉素甫·吐拉克.量子弱测量理论及其应用[D].北京:中国科学院研究生院,2012.

　　[7] Aharonov Y, Albert D Z, Vaidman L. How the Result of a Measurement of a Component of the Spin of a Spin-1/2 ParticleCan Turn Out to be 100[J]. Physical Review Letters, 1988, 60(14):1351-1354.

　　[8] Vijay R, Macklin C, Slichter D H, et al. Quantum Feedback Control of a Superconducting Qubit: Persistent RabiOscillations[J]. Physics, 2012.

　　本文来源于科技期刊《电子产品世界》2019年第8期第58页，欢迎您写论文时引用，并注明出处