基于FPGA的椭圆曲线加密设计

　　摘 要： 椭圆曲线加密是一种目前已知的所有公钥密码体制中能够提供最高比特强度的一种公钥体制。在FPGA实现椭圆曲线加密系统时，基于GF(2)的多项式有限域中的乘法、求逆运算是其中的两大难点。本文提供了一种椭圆曲线加密的FPGA实现的结构，着重讨论了基于GF(2)的多项式有限域中的乘法、求逆运算的实现，并与软件实现的性能进行了比较。

　　加密的安全性

　　从数论的角度来说，任何公钥密码系统都建立在一个NP(无法处理的问题)的基础上，即对于特定的问题，没有办法找到一个多项式时间算法求解该问题。一般求解此类问题的算法都是指数时间或者亚指数时间，例如现在常用的RSA算法就是基于大整数因式分解问题的难解性。经过近三十多年的研究，RSA算法虽然并不存在多项式时间的算法，但是可以找到亚指数时间的算法，目前其密钥长度必须大于1024位才能保证信息传递的安全，而椭圆曲线加密系统 (EllipTIc Curve Cryptosystem—ECC) 是目前已知的所有公钥密码体制中能够提供最高比特强度 (Strength-Per-Bit) 的一种公钥体制，只需要160的密钥就可以达到1024位RSA算法提供的安全等级。其根据是有限域上的椭圆曲线上的点群中的离散对数问题(ECDLP)，许多密码专家认为它是指数级的难度。因此对于椭圆曲线加密系统来说，这一点从计算量、处理速度、存储空间和通信带宽等角度分析，椭圆曲线加密系统都有很大的优势。IEEE已经制定的公钥加密算法标准P1363就是基于ECC算法的。现在密码学界普遍认为它将替代RSA成为通用的公钥密码算法，目前已成为研究的热点，是很有前途的研究方向。

　　图1 点算法实现

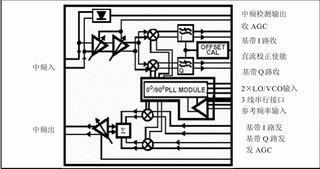
　　图2 密钥、数据交换

　　图3 椭圆曲线加密系统结构图

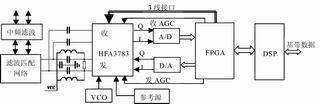
　　图4 椭圆曲线加密系统FPGA电路模块框图

　　图5 验证系统结构

　　椭圆曲线加密体制

　　椭圆曲线

　　引进Non-supersingular椭圆曲线Weierstrass方程E:Y2+XY=X3+aX2+c其中a,c∈GF(2k),c≠0。为简化以后的运算，引进z使X=x/z;Y=y/z，则椭圆曲线方程化为E:y2z+xyz=x3+ax2z+cz3，定义(x, y, z)=λ(x, y, z)。可以看出当z≠0，(X, Y)和(x, y, z)相对应，当z=0可以理解为沿y轴趋向无穷远，定义为无穷远点O。则椭圆曲线上所有的点外加无穷远点构成的集合构成一个Abel群，O是单位元(零元)。在椭圆曲线E上定义了两种点运算：点运算和点运算。

　　1) 椭圆曲线上点运算定义为：设P=( x1, y1, 1)∈E，Q=( x2, y2, 1) ∈E，-P=( x1, y1+ x1, 1), 当Q≠-P时 PQ=(x3, y3, z3) 则

　　当P≠Q时：

　　其中A=(x2z1+x1),B=(y2z1+y1), C=A+B,D=A2(A+a2z1)z1BC

　　当P=Q时：

　　其中

　　2) 椭圆曲线上的点运算定义为：设P=(x1, y1, 1)∈E，(ltlt-1...l0)2是整数l的二进制表示形式，lP=PPAP=Q且Q∈E。

　　利用上面的点运算，得点算法实现如图1所示。定义l=logpQ，若P的周期很大，则利用l、P求Q是比较容易的，但利用P、Q求l是很难处理的，这就是ECDLP，椭圆曲线加密就是建立在这个难题之上。

　　加密体制

　　在Diffe-Hellman公钥系统体制中，具体的椭圆曲线、曲线上点P及P的周期大素数N都是公开信息。

　　A和B要进行通讯，首先得到椭圆曲线E、点P及素数N。然后用户A将[1,N-1]中随机选取的整数a作为私钥，A将KpubA=aP作为自己的公钥传送给用户B，与此同时B将 [1,N-1]中随机选取的整数b作为私钥，并将KpubB=bP作为自己的公钥传送给A。A、B各自将自己的私钥点乘于对方传过来的公钥得到KAB，这样就完成了密钥的交换过程。当用户A需要将待传数据m传送给用户B时，A利用m和KAB生成Em，当用户B得到Em后，利用密钥交换过程自己生成的KAB和从用户A处得到的加密数据Em生成数据m。见图2。

　　椭圆加密体制实现

　　迄今所投入使用的椭圆加密系统中，绝大部分的密钥长度都比较短，一般集中在30~60位，这是因为在软件实现时，由于软件执行速率所限，密钥长度比较大(≥160)的椭圆加密系统的速率将达不到使用要求。与此同时，在硬件实现时，密钥长度比较大的椭圆加密系统将耗费大量的硬件资源。随着椭圆加密算法研究的深入和可编程逻辑器件的快速发展，利用可编程逻辑器件实现椭圆加密系统已经是一个可能的选择，下面将介绍一种实现方案，并且用软、硬件分别实现。

　　根据以上椭圆加密体制的要求，设计出图3的加密系统结构图，其中椭圆加密系统参数接口获取与加密有关的椭圆的基本参数，如私钥、椭圆曲线、椭圆曲线上的给定点等。椭圆曲线乘法控制部分主要负责如何计算乘法结果，会大量调用PP和PQ来实现乘法功能;而PP和PQ通过有限域加法、乘法和求逆的调用得到结果。

　　软件模型验证

　　软件实现的主要目的是为硬件实现建立验证模型，整个软件的结构如图3所示。在软件验证系统实现的过程中，有限域上的加法是异或操作。有限域上的乘法和求逆是关键点，必须预先考虑到硬件实现时的资源消耗，需要高效的算法。在此系统中使用了复合域GF((2n)m)带来的特殊性，可以高效、快速的实现乘法和求逆运算。

　　* GF(2n)上的乘法：A(y)&TImes;B(y)=C(Y)modQ(y)，Q(y)为既约多项式。常用的有： Paar-Rosner乘法器、Mastrovito乘法器、Massey-Omura乘法器、Hasan-Bhargava乘法器等，此处介绍两种选择：

　　1) 当n比较小时可用查表法实现，设ω为Q(y)=0的本原根，则F2n={0,ω,Aω2n-1}，利用查表法取得A、B的级次数a、b，C的级次c=a+b，再次利用查表法由c得C。在本系统中就使用了此法实现GF(2n)上的乘法。

　　2) 当n比较大时，利用查表法资源消耗太大，难以承受，可利用C=Z&TImes;B(n比较大时)，Z是由A(y),Q(y)确定的矩阵，其中：

　　* 复合有限域的乘法：以GF((24)2)为例，利用GF(24)上的乘法和加法可以构造出GF(28)的乘法。子域GF(24)的本原多项式为Q(y)=y4+y+1，第二个子域的本原多项式为R(z)=z3+z+ω14，其中ω是GF(24)的基底元素，满足Q(ω)=0。域中两个元素的乘法[a0+a1z]&TImes;[b0+b1z]可以表示为：

　　这样GF((24)2)在复合域上的乘法就可以通过GF(24)上的有限域的数学运算而得到。

　　* 复合有限域的逆运算：复合有限域GF((2n)m)中的元素A的逆为：

　　其中

　　可以观察到Ar属于子域GF(2n)中的元素，可以较容易的求取(Ar)-1的值。

　　FPGA硬件实现

　　软件化的实现方法开发时间短，但是其加密速度比较慢，妨碍了椭圆曲线加密的实用性。FPGA的方法综合了软件的灵活性和硬件的安全性，提供了比软件化方法优越的速度，和传统的ASIC实现相比，可编程器件由于其高度的灵活性，更适合于密码学的应用领域。

　　在软件模型的基础上，我们针对FPGA硬件的特性对模型进行了优化。根据椭圆曲线加密算法的要求，对加密系统进行模块化设计，每个模块独立完成其各自功能，模块之间进行相互数据交换以及时序控制，达到加密功能。图4是椭圆曲线加密系统FPGA实现的电路模块框图。

　　其中，椭圆曲线加密控制系统模块是整个系统的核心。当Ready为True时，系统读入初始数据并且控制RAM进行初始数据的存储。在运算过程中，该模块根据数据源对选择器进行控制循环，进行PP=R和PQ=R运算，获得最后结果，然后通过Out_Ready信号对结果进行输出;选择器模块根据控制系统模块提供的指令对PP=R模块和PQ=R模块进行控制，并且提供相应的实时数据流;PP=R模块和PQ=R模块利用对有限域上的加法和乘法运算进行时序控制求出椭圆曲线上点的加法运算，将直接影响到整个系统的速度性能，因此必须对有限域上的加法和乘法运算设计合理的输入输出数据流，以达到高效率的运算速率。各种存储器模块根据不同的指令分别存放系统的初始值、运算过程中的中间值以及系统运算结果。

　　综合以上各种因素，我们选择了XILINX 公司的VirtexII器件，ISE 4.1作为开发平台，VHDL作为开发语言。由于168位的椭圆曲线加密算法的计算量比较大，所以在FPGA实现的时候，布线是个值得考虑的因素。对于FPGA器件的选择应考虑到布线资源，Virtex 系列提供的布线资源比较丰富。在Modelsim上进行仿真后得到性能指标为：在40MHz时钟驱动下第一次加密或者解密时需要初始的建立时间，明文或者密文的输出需要2ms左右，其后的明文或者密文的输出大约为25Mbps。可以看出，这是一个比较高的速率，可以应用于很多场合。

　　应用系统验证

　　椭圆加密硬件实现后，必须在实际系统中得到验证。我们特地构造了串口加密实验板进行验证，整个验证系统的结构如图5所示。经过实际系统验证，证明上述椭圆加密体制硬件实现是成功的。

　　结语

　　公钥密码体制由于其运算和时间复杂性较高，通常用于密钥管理、密钥交换、数字签名和认证等涉及信息较少的场合。目前，被广泛使用的仍是DES、RSA这样陈旧的算法，算法的更新不仅可以使本来的密码户获得更好的性能，而且还可以使IC卡、手机等本来难以实现密码算法的领域可以使用密码技术来保证信息安全。

　　椭圆曲线密码体制(ECC)正在以其更短的密钥和理论上更高的强度引起业界的重视，而椭圆曲线密码体制(ECC)的硬件实现也将是公钥密码体制中的一个聚焦点。本文虽然已经为将来的工作打下了良好的基础，在以下几个方面还有大量的工作需要做。首先是可编程逻辑器件的发展，以后必然出现能提供更大门数，能提供更快速率的器件;其次是椭圆曲线密码体制本身的改进;最后是有限域数学运算的硬件实现算法的进一步改良。随着以上各个方面的发展，将能提供更长密钥和更快的数据速率的硬件实现，为国民经济和社会发展提供更快更安全的加密系统。