基于LMS算法的回声消除系统仿真研究
用远端语音信号作为参考信号来跟踪回声信号，得到滤波器的输出信号
，两者相减，得到误差信号为
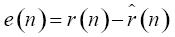。误差信号的波形如图7所示。从图中可以看出，收敛时间大约在8000个点左右，之后的误差曲线接近于0，仿真效果非常理想。
根据上文分析可知，标准LMS算法的失调系数和滤波器的输入功率成正比，因此如果输入信号功率比较大，那么自适应滤波器将产生梯度噪声放大的现象。如果对步长因子取适当的值，使其反比于输入信号能量，那么失调系数将会保持不变，因此可以进行如下假设[11]：
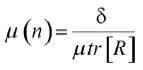(10)
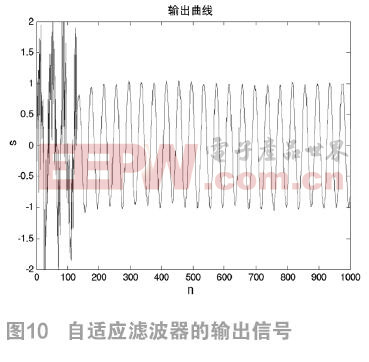
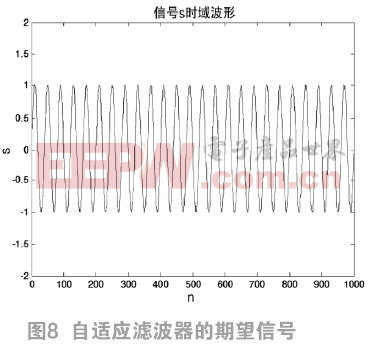
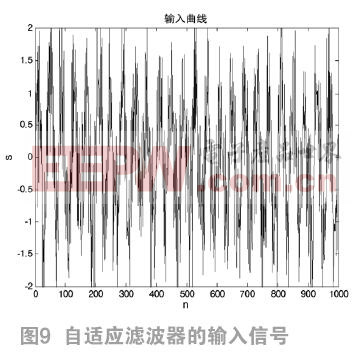
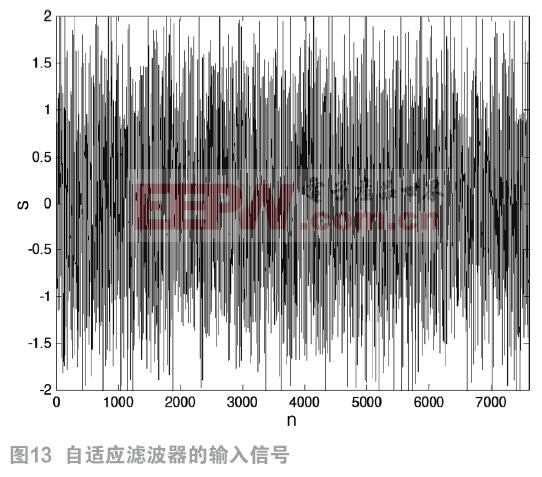
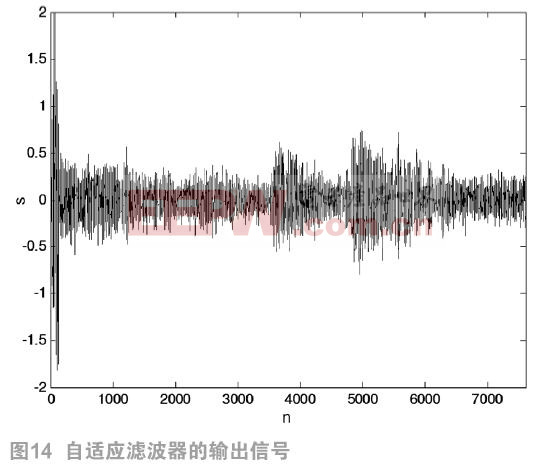
用MATLAB生成一个幅度为1，角频率为0.05的单频正弦信号r(n)作为滤波器的目标输出信号，如图3.7所示。再生成一个信噪比为3db的白噪声信号y(n)作为远端输入信号，如图8所示。取变步长LMS算法的步长因子为1，自适应滤波器的输出信号如图9所示。两者相减得到误差信号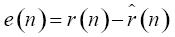，如图10所示。
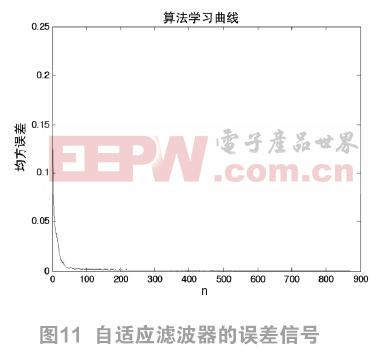
根据上述结果可知，在滤波器的输入信号和目标信号的参数相同时，变步长LMS算法具有更快的收敛速度。同样地，上述仿真的目标信号是单一频率的正弦信号，很难代表一般性，所以下面用真实的语音信号作为目标信号来进行仿真实验。
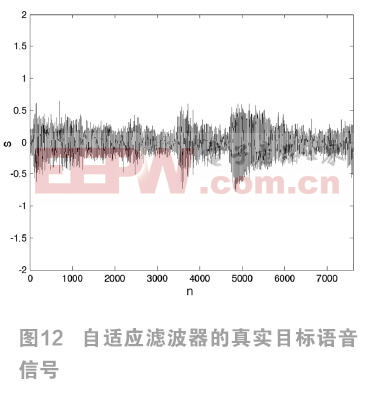
比较预期输出信号的波形和实际输出信号的波形，可以看出滤波器的实际输出信号的变化曲线和预期输出信号的变化曲线同步。
3 结论
经过MATLAB仿真可以看出，使用变步长的LMS算法时，收敛以后得到一条误差为0的曲线。收敛情况比使用普通LMS算法好，可以将回声完全消除。目前，正在研究基于该算法的回声消除硬件平台。
参考文献：
[1]刘德全.基于微麦克风阵列的声学回声消除算法研究及软件仿真[D].电子科技大学, 2012.
[2]王树成. 最小均方算法的改进及应用研究[D].华东交通大学,2013.
[3]张子刚. 一种双端通话检测算法中噪音阈值自动更新的方法[D].复旦大学,2013.
[4]赵彤,梁家碧,夏天翔,邹亮,张黎.基于LMS自适应滤波算法的电力变压器有源降噪系统[J].高电压技术,2016,42(07):2299-2307.
[5]张红梅,韩万刚.一种新的变步长LMS自适应滤波算法研究及其应用[J].仪器仪表学报,2015,36(08):1822-1830.
[6]王树成. 最小均方算法的改进及应用研究[D].华东交通大学,2013.
[7]张子刚. 一种双端通话检测算法中噪音阈值自动更新的方法[D].复旦大学,2013.
[8]李杨,韩鹏,檀虎.几种变步长LMS算法的性能分析与比较[J].国外电子测量技术,2013,32(03):28-30.
[9]马伟富. 自适应LMS算法的研究及应用[D].四川大学,2005.
[10]汪萌,戴礼荣,宋彦,王仁华.一种使用双滤波器的回声消除算法[J].数据采集与处理,2006(01):74-79.
[11]蔡宇,洪缨,原建平,侯朝焕,郝程鹏.语音系统中的子带自适应回声消除技术[J].仪器仪表学报,2013,34(07):9-14.
本文来源于《电子产品世界》2018年第10期第64页，欢迎您写论文时引用，并注明出处。
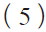
评论