数字匹配滤波器的递归折叠实现

　　针对数字匹配滤波器（DMF）的FPGA实现提出一种优化结构。利用16位移位寄存器（SRL16E）的存储潜力，设计递归延迟线（RDL）;再利用RDL抽头个数倍减而抽头样本速率倍增的特点和时分复用技术，提出DMF的递归折叠结构。该结构以提高工作时钟频率为代价，增大延迟线的采样率以及相关运算单元的吞吐率，从而成倍降低DMF的资源消耗。当采用l/4递归折叠结构时，资源消耗仅为优化前的l/3.

　　随着直接序列扩频（DSSS）通信技术和软件无线电技术的发展，全数字扩频接收机成为研究的热点。数字匹配滤波器（DMF）是全数字扩频接收机的核心部件，它主要用于伪码（PN）快速捕获和解扩。传统的DMF设计效率较低，当PN码码长较长时，需要占用较多的FPGA资源，成本较高。作者通过改进延迟线的结构，并结合时分复用技术，提出DMF的递归折叠结构，该结构极大地降低了DMF的资源消耗。

　　1 DMF的基本结构和参数

　　DMF是一种抽头间隔即码片周期为Tc、抽头系数为扩频序列（取值为±1）的特殊的FIR滤波器。其直接型结构由延迟线和相关运算单元（CCU）构成，如图1所示.

　　延迟线用于保存相关时间范围（LTc）内的所有输入样本，它由L个延迟单元组成。虽然级联多个D触发器是实现延迟单元的最简方法，但它将大量使用D触发器，因此不宜用于构建量化位数大、阶数高的DMF延迟线.FPGA拥有丰富的查找表（LUT）资源，它可以用16位循环移位寄存器（SRL16E）实现 l～16个节拍的信号延迟。对于M bit量化、过采样倍数R≤16的DMF来说，构造一个延迟单元需要M个SRL16E.

　　如图1所示，相关运算单元由L个乘法器和一个倒金字塔形的加法树组成。加法树的第1级有L/2个（M+1）bit二输入同步加法器（参与运算的是延迟抽头样本，字长为M bit，为了防止计算溢出，在相加之前需要进行1 bit的符号位扩展）、第2级有L/2个（M+2）bit二输入同步加法器，……，整个加法树有L- 1个二输入同步加法器。

　　DMF的量化位数、输入采样率以及工作频率是影响DMF性能的3个关键参数，后两个参数是优化结构的基础，需要仔细权衡。

　　DMF的输入为数字下变频器的输出（数字解调方案）或者模拟基带ADC的输出（模拟解调方案），其量化位数一般都为8 bit以上.DMF的资源消耗近似正比于量化位数，因此需要在这两者之间做出适当的折衷。文献中给出了DMF的量化精度对解扩性能的影响及DMF量化位数的选择依据。一般认为高斯信道下DMF选择3 bit量化较为合适，此时量化误差造成的性能损失不大，再增加量化位数并不能明显改善系统性能。为了叙述的一般性，定义DMF的输入量化位数为M.

　　采样率是全数字接收机的关键参数之一，为了降低实现难度，避免采样率变换环节，DMF的采样率一般为接收机中频或基带ADC的采样率。为了降低对ADC前端模拟滤波器性能的要求并提高PN码同步精度，需要提高采样率。然而采样率的提高将增加接收机的运算量，从而导致占用更多的FP-GA资源，因此同样需要折衷考虑。工程上采样率一般是chip速率的整数倍，用过采样倍数R表示，R值一般取4～8.

　　模块的数据处理能力与其并行程度（取决于硬件规模）和吞吐率（取决于工作频率）成正比。在额定数据处理能力下，提高模块的工作频率可以降低对模块并行程度的要求，即工作频率和设计规模是可以互换的。目前主流的高端FPGA的工作频率可以达到200～400 MHz，远远高于DMF的采样率，采用时分复用方式将大大降低硬件资源消耗量。

　　作者提出的递归折叠型DMF，充分利用SRL16E的存储潜力，用递归结构降低延迟线的资源消耗，然后利用递归延迟线具有抽头个数倍减而抽头样本速率倍增的特点来时分复用相关运算单元，从而降低乘法器和加法器的数量。上述措施可成倍降低DMF消耗的硬件资源。

　　2 递归延迟线的结构与特点

　　传统的延迟单元用SRL16E实现R（R≤16）位移位寄存，在每个采样周期Ts内，延迟单元中的R个样本全部右移一位，这样，输入样本经过R×Ts后送到抽头处，从而实现了Tc时延.R位移位操作未能充分利用SRL16E的存储潜力，为此作者提出递归延迟线结构。在该结构中，无论R取何值，SRL16E 都进行16位移位操作。这样保存L×R个输入样本总共需要M×L×R/16个SRL16E，仅为传统结构的R/16.下面结合图2进行时序分析.

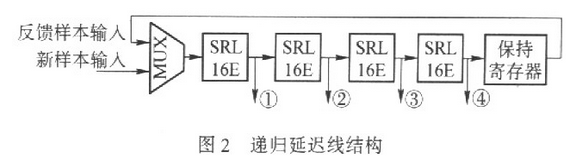
　　由于SRL16E进行16位移位操作，为了保证其时延等于Tc，移位周期必须为Tc/16.把R×Ts/16定为延迟线的工作时钟周期，那么工作时钟频率为chip速率的16倍，即采样率的C倍，其中C△16/R，因此每C个工作时钟周期才输入一个新样本。不妨假设新样本在第nC个工作时钟周期（后面简称为时刻）到来，其中n为整数。如果时刻m是C的整数倍，MUX把新样本推入延迟线，否则MUX把保持寄存器中的旧样本反馈到延迟线的输入端。

　　在nC时刻被MUX推入到延迟线入口的样本，在经过L×R个时钟周期后将在nC+L，×R时刻被推到保持寄存器中，然后在nC十L×R+l时刻（因为该时刻不是C的整数倍）将再次被送入到延迟线的入口，……;当该样本第C次进入保持寄存器后，已是C（L×R+n+1）时刻，此时.MUX将选入一个新的样本，而它将被抛弃。这样一个新样本在递归延迟线中刚好循环C次，历时C（L×R+1）时钟周期，从而实现了L×Tc+Ts时间的延迟。

　　下面分析递归延迟线各抽头的输出样本在时间上的相位关系。设nC时刻输入样本为x（n），那么抽头①～④处的输出样本应该是x（n- R），x（n2R），x（n-3R）和x（n-4R）;nC+1时刻延迟线输入的应该是已经延迟L×R+1时钟周期的样本，即x（n-L×R/C）;抽头 ①～④处的输出样本应该是x（n-R- L×R/C），x（n-2R-L×R/C），x（n- 3R-L×R/C）和x（n-4R-L×R/C）;第nC+c（0≤c≤C-1）时刻延迟线输入的应该是已经延迟c（LR+1）时钟周期的样本，即 x（n-c×L×R/C）。那么抽头①～④处的输出样本应该是x（n-R-c×L×R/C），x（n-2R-c×L×R/C），x（n-3R- c×L×R/C）和x（n-4R-c×L×R/C）。

　　可以看出，同一个抽头在相邻2个时刻输出的样本相差L×R/C个采样点，即1/C个码周期。这样递归延迟线把一个码周期内的信号样本分解到C个相位上，并在C个时钟周期内依次串行输出，从而以多相的方式实现了信号延迟的功能。

　　递归延迟线仅需L/C个延迟单元即可实现L×Tc时延，它以工作时钟频率提高C倍为代价，将资源消耗量压缩到优化前的1/C.例如，当R=4时，C=16/R=4，即资源消耗仅为原先的25%.

　　3 递归折叠DMF

　　3.1 递归折叠DMF的结构

　　递归延迟线不仅使抽头数减少到优化前的1/C，而且使抽头的样本输出速率增大C倍。与之对应，相关运算单元中乘法器和加法器的个数分别从L和L-1减少到 L/C和L/C-1，同时工作频率提高C倍。在C个工作时钟周期内，相关运算单元根据递归延迟线分解的信号相位，依次计算出C个相位上的接收信号与PN序列的部分相关值，并利用累加器完成部分相关值的合并，从而得到完整的相关值。根据这个思路，作者提出递归折叠结构的DMF如图3所示。

　　该结构在递归延迟线的基础上，折叠使用相关运算单元，从而用一个L/C抽头的DMF完成L阶匹配滤波运算。

　　图3是一个1/2递归折叠滤波器，其参数为：L=8，R=8，C=2用1个4抽头DMF时分复用实现了8阶匹配滤波。时序分析与上节相似。不失一般性，假设在偶时刻输入新样本，那么在第0，2，4，6，…时刻MUX将输入样本推入延迟线，在第1，3，5，7，…时刻，MUX将保持寄存器中的样本反馈到延迟线的入口。经过一段时间后，某个抽头在偶时刻的样本与其在下一时刻输出的样本在相位上将相差半个码相位周期，因此在相邻的时钟周期内，加载到各抽头的乘法系数也相差半个码相位周期。累加器合并奇、偶时刻的部分相关结果，从而得到完整的结果.

　　图4为l/4递归折叠滤波器的结构框图。（参数为L=8，R=4，C=4）。时序更加复杂，在相邻时钟周期内，抽头样本之间的相位差为1/4码周期.

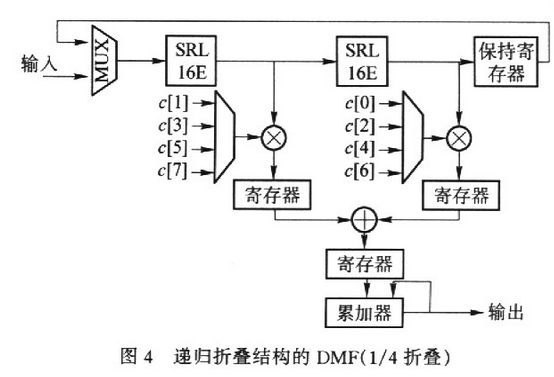
　　3.2 递归折叠DMF与传统DMF资源消耗对比

　　为了评估优化效果，表1给出了采用基本结构和改进的折叠结构实现DMF所消耗的资源（L=256，M=4，R=4，采样率为fs）.

　　从表1可以看出，除了需要1个额外的累加器以及L/C个C输入数据选择器之外，递归折叠DMF所消耗的资源（包括SRLL6E、乘法器和加法器）压缩到接近未优化结构的l/C，但是其工作时钟频率也提高到原来的C倍，这也证明了硬件规模和工作频率可以互换。

　　然而工作时钟频率的提高是有限制的，更高的工作频率要求采用档次更高的FPGA或者需要在FPGA的细节实现中付出更高的代价，因此在设计递归折叠DMF 时，需要统筹考虑chip速率、过采样倍数和FPGA的工作时钟频率。例如。对于xilinx Virtex2系列FPGA，当chip速率不超过10 MHz/s时，可以选用1/4或者l/2递归折叠结构，此时工作频率不超过160 MHz，时序要求适中。

　　4 结束语

　　利用工作时钟频率与设计规模可互换的原理，通过递归延迟线、折叠相关运算单元以及时分复用技术，使递归折叠结构大大降低了DMF的资源消耗。该结构已经应用于某型号中频数字化直接序列扩频接收机中，应用结果表明优化效果明显。在采样率为40.96 MHz，工作时钟频率为163.84 MHz的条件下，通过4倍时分复用，其资源消耗约为优化前的l/3.