基于安芯一号的六轴姿态控制板设计
一、项目设计背景及概述
本文引用地址:http://www.amcfsurvey.com/article/201710/367179.htm在许多工程应用中,都需要测量载体与水平面的倾斜角度。对于导航定位系统来说,姿态信息更是一个重要参数。本系统主要目标是在动态情况下通过姿态融合得到精确的俯仰角和横滚角。首先采用加速度传感器测量倾斜角度,并对测量角进行数据预处理以减少误差,其次加入陀螺仪进行姿态融合,主要方法为卡尔曼滤波,得到系统的横滚角和俯仰角。该方法广泛应用于工程中,技术成熟,姿态融合效果良好。
惯性测量单元在飞行器制造、传感器技术领域都能见其身影,应用前景十分广泛。一般的,一个IMU包含了三个单轴的加速度计和三个单轴的陀螺,加速度计检测物体在载体坐标系统独立三轴的加速度信号,而陀螺检测载体相对于导航坐标系的角速度信号,测量物体在三维空间中的角速度和加速度,并以此解算出物体的姿态。在导航中用着很重要的应用价值。
为了提高可靠性,还可以为每个轴配备更多的传感器。一般而言IMU要安装在被测物体的重心上。IMU大多用在需要进行运动控制的设备,如汽车和机器人上。也被用在需要用姿态进行精密位移推算的场合,如潜艇、飞机、导弹和航天器的惯性导航设备等。利用三轴加速度计,受外力加速度影响很大,在运动/振动等环境中,输出方向角误差较大。加速度测量的是重力方向,在无外力加速度的情况下,能准确输出ROLL/PITCH两轴姿态角度,并且此角度不会有累积误差,在更长的时间尺度内都是准确的。但是加速度传感器测角度的缺点是加速度传感器实际上是用MEMS技术检测惯性力造成的微小形变,而惯性力与重力本质是一样的,所以加速度计就不会区分重力加速度与外力加速度,当系统在三维空间做变速运动时,它的输出就不正确了。
二、项目设计原理
1、 原理概述
陀螺仪输出角速度,是瞬时量,角速度在姿态平衡上是不能直接使用,需要角速度与时间积分计算角度,得到的角度变化量与初始角度相加,就得到目标角度,其中积分时间Dt越小,输出角度越精确,但陀螺仪的原理决定了它的测量基准是自身,并没有系统外的绝对参照物,加上Dt是不可能无限小,所以积分的累积误差会随着时间流逝迅速增加,最终导致输出角度与实际不符,所以陀螺仪只能工作在相对较短的时间尺度内。
所以在没有其它参照物的基础上,要得到较为真实的姿态角,就要利用加权算法扬长避短,结合两者的优点,摈弃其各自缺点,设计算法在短时间尺度内增加陀螺仪的权值,在更长时间尺度内增加加速度权值,这样系统输出角度就接近真实值了。
2、 硬件设计原理
2.1加速度计模块
图2.1为加速度传感器模块电路图。加速度计选用Analog Device(亚德诺半导体)公司的ADXL345,该传感器是一款三轴数字加速度传感器,其感应精度可达3.9mg/LSB,倾角测量典型误差小于1°,且感知加速度的最大范围是 16g。具有超低功耗、采样速率可调、测量模式可调等特点。在实际使用过程中,一般设置感应范围为 2g,感应精度为3.9mg/LSB,这样可以提高输出数据的稳定性,满足系统加速度范围和精度要求。它可以在倾斜检测应用中测量静态重力加速度,还可以测量运动或者冲击导致的动态加速度。
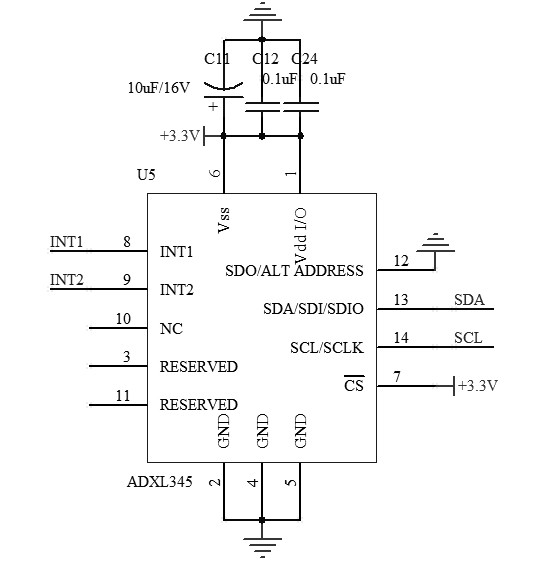
图2.1 加速度计模块原理图
2.2陀螺仪模块
陀螺仪采用InvenSense(应美盛)公司的ITG3205。图2.2为陀螺仪模块的原理图设计。该芯片用于测量绕三轴转动的角速度值,是一个数字输出的将X、Y、Z三轴角速度传感器整合在单一电路上的三轴陀螺仪。其特性在于运用了三个16位A/D转换器来数字化陀螺仪输出端,有程控的内建低通滤波器带宽,以及快速模式的IIC接口。除此之外,还有内建温度传感器以及精准差仅为2%的内建震荡设计。
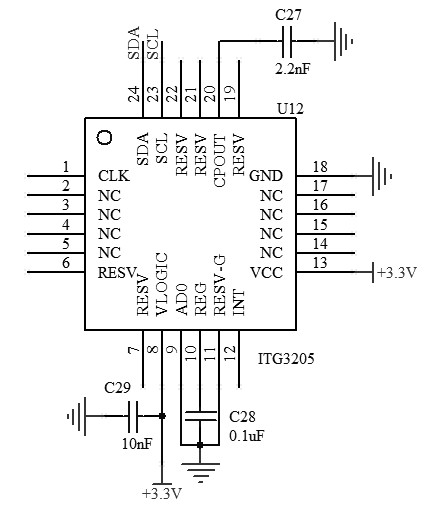
图2.2 陀螺仪模块原理图
陀螺仪可以测量载体角速度,具有高动态特性,但是它是一个间接测量器件,它测量的是角度的导数(角速度),所以必须要将角速度测量值对时间积分才能得到角度。
3、 软件设计原理
系统上电后完成一系列初始化步骤后便进入工作状态。分别对三轴加速度计、三轴陀螺仪进行数据的采集与补偿,通过加速度计与陀螺仪的姿态融合,得出载体在静态与动态条件下都准确的俯仰角和横滚角。系统软件采用模块化设计,根据不同的功能采用不同的程序块,可以简化编程,使系统结构清晰,同时,可以增加代码的重用性,便于实现功能扩展。
三、项目设计框图
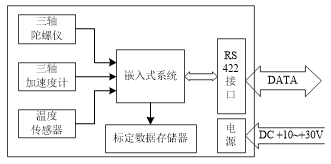
1、硬件设计框图
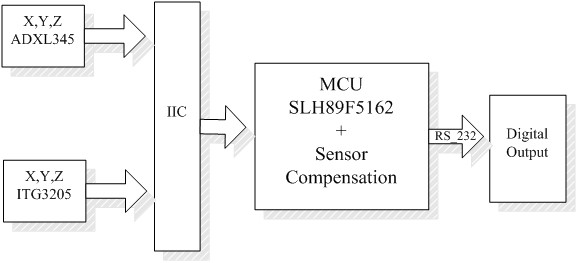
图3.1 硬件设计框图
2、软件设计框图
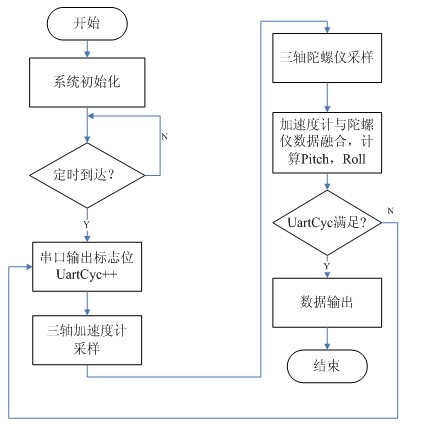
图3.2 软件设计流程图
3、姿态融合算法框图
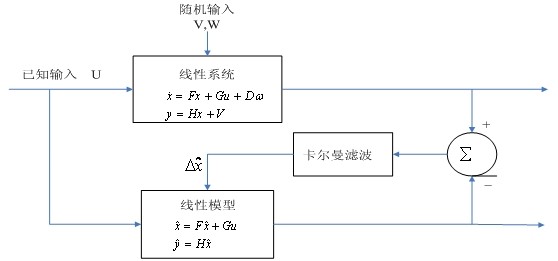
图3.3 卡尔曼滤波结构框图
四、测试结果
项目达到的关键硬件指标
4.1系统实物图片
PCB正面图:

PCB反面图:
项目实物图:

4.2姿态融合效果分析
系统采用卡尔曼滤波函数进行加速度计与陀螺仪的姿态融合。图4.1所示为姿态融合前的系统水平时横滚角输出曲线图,即仅由加速度计ADXL345计算得到的角度。该组实验在动态条件下完成,即保持载体与水平面角度不变的前提下(在此测试横滚角,并取角度值为0°),人为给系统施加外力作用,使系统受到外部加速度干扰,同时记录数据绘制曲线。从图中可以看出,在系统受到外力作用下,数据精确度大大降低。图中最大误差达到50°。
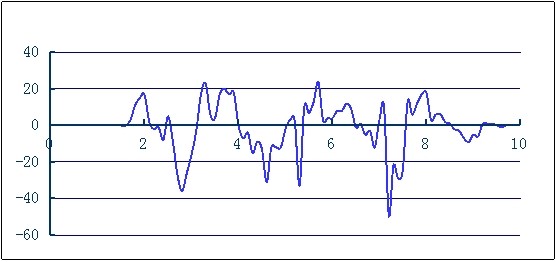
图4.1 姿态融合前横滚角输出曲线图
图4.2所示为姿态融合后的系统水平时横滚角输出曲线图。从图中可以看出,即使系统受到外部加速度的干扰,仍能保持横滚角在0°及0°附近很小的范围内波动。最大误差仅有1°。姿态融合算法有效减小了动态条件下的系统误差。
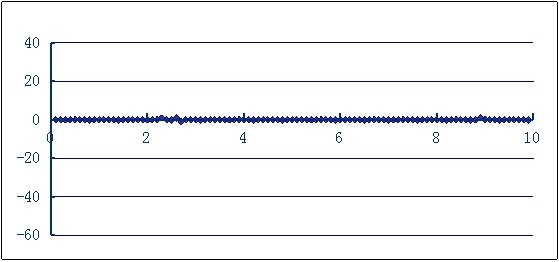
图4.2 姿态融合后横滚角输出曲线图
视频网址 http://pan.baidu.com/s/1dDoW0d7



.jpg)






评论