一种基于支持向量机的车型自动分类器设计方案

车型自动分类一直是智能交通领域中的一个热点问题。自动识别车辆类型对实现交通管理智能化具有重要意义。目前已经广泛应用的分类方法是采用地感线圈根据不同类型车辆通过线圈产生的电磁感应曲线不同这一原理进行分类。这种方法分类速度较低，误差较大，因此难以满足不停车收费系统的要求。

随着计算机硬件性能的不断提高，基于图像处理的车辆分类方法逐渐得到重视，计算机对摄像机捕捉到的车辆图像进行处理得到车辆的外形信息，这些信息可以作为车型识别依据进行车辆分类。已经采用的数据分析方法有模式匹配和BP神经网络两种。前者是将得到的外形信息与系统中的车型模式库进行比对，输出匹配度最大的模式类型作为车辆类型[1]；后者是将车辆信息输入到已训练好的神经网络分类器进行分类[2]。基于模式匹配的分类方法实现原理简单，但是选择合适的模式比较困难；采用BP神经网络的分类方法中，由于BP神经网络本身存在网络结构无规律可循、作用机理不明确并易陷入局部极小值等缺陷从而限制了这种方法的应用。

支持向量机是二十世纪90年代提出的一种新的学习机[3]，具有较好的推广能力和非线性处理能力。本文给出一种基于支持向量机的车型分类器的设计方案。

1 支持向量机识别理论

设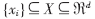为输入空间的某类别数据集，对于非线性可分情况而言，类别的边界比较复杂。引入从输入空间X到高维空间Y(特征空间)的非线性变换Φ将会简化类别边界。Φ可以把X中具有复杂几何形状的类边界(覆盖该类别全部数据集)映射为Y中的规则球(覆盖变换后的相应类别全部数据集)。如果希望输入空间X中类的边界紧致包围本类数据集，就要在变换后空间Y中寻找最小的闭合球。Y中的闭合球表述为：


其中∣∣●∣∣为欧式范数，a为球心。目标就是通过搜索所有满足约束条件的a来最小化R2。
构造Lagrange函数如下：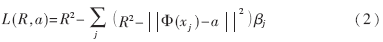


这里βj≥0，是Lagrange乘子。达到极小值的必要条件为：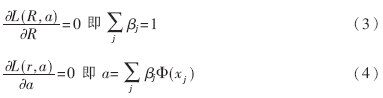


把式(3)和式(4)代入式(2)消去r和a，就转化为它的Wolfe对偶问题：求式(5)中W关于变量βj的极大值。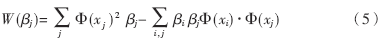

在W达到极大值时，对于球内的数据和部分球上数据，βj=0；对于位于球边界的数据，βj＞0。满足βj＞0的数据就是支持向量，它们定义了球的中心,如式(4)。

可以采用合适的Mercer核函数替代内积Φ(xi)·Φ(xj),

目前主要的核函数有两种：

阶次为d的多项式核函数


其中C＞0为常数。位于球内(包括球上)的数据点，有ζj=0和βj＜C；对于孤立数据点βj=C。
定义输入数据点x映射到特征空间内时到球心距离为:


如果R(x)＞R,那么x为孤立点或其它类点。

2系统实现

2.1图像采集和特征提取

利用两部CCD摄像机和图像采集卡获得同一车辆的两幅图像，基于双目视觉原理对两幅图像进行特征匹配，得到车辆的三维模型。根据摄像机标定矩阵和成像几何模型可以计算出车辆的三维数据：车长、车宽和车高。采集每一类别车辆图像若干，得到该类车辆训练样本作为车型分类器训练依据。

2.2 训练数据预处理

采用有导师训练的方法进行分类器训练，首先要确定训练样本所属类别。本文将车辆分为大型、中型和小型三类。按照前述方法获取100个车辆三维数据对，采用动态聚类方法K-Means对100个数据样本进行自动聚类[5]，设定聚类类别数为3。从聚类结果选择各类训练样本(每类10个)，其余数据作为测试样本，训练样本见表1。

2.3 分类器设计

支持向量机一般用于二类模式识别，对于多类问题识别能力不足。为了使二类分类器能用于多类模式,本文为每类车辆分别设计识别器，然后通过表决器进行决策，如图1。

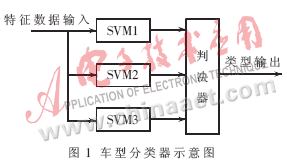
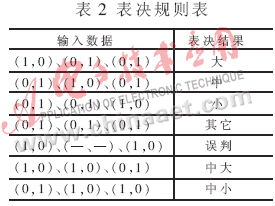
其中，SVM1、SVM2和SVM3分别为大、中和小型车的识别器，输出结果分别为(大，非大)、(中，非中)和(小，非小)三个数对。表决器以三个识别器的输出组成的向量作为输入进行综合判断，输出车辆类型。表决器的表决表见表2。

对于每个SVM识别器，遵循了相同的设计原则：首先采用有导师训练的方法进行训练，选择合适的参数q和C；然后使用测试样本测试识别率。

本文以小型车识别器SVM3为例说明SVM识别器的训练过程。

(1)标号：把属于小型车的训练样本标记为类别1，其余训练样本均标记为类别0；
(2)训练：选择参数q和C进行循环,计算目标误差；
(3)结束：当目标误差小于0.001时结束循环；
(4)调整：根据训练结果，调整参数q和C;
(5)重复步骤(2),直到得到满意的训练结果为止。

通过反复试验发现，参数q影响识别器分类边界的复杂性，q越大分类边界越复杂,即支持向量个数越多；参数C的取值变化改变识别器对本类样本数据异常的容忍度，C越小容忍本类异常数据的能力越差。当20≤q≤70时，识别器识别类1所用的支持向量数为3且保持不变，因此令q为45(C=1)。支持向量分别为(0.33 0.1405 0.141)、(0.33 0.1405 0.144)和(0.488 0.18 0.145)类似地，选取中型车识别器q为60(C=1)，识别中型车所用支持向量个数为5，分别为(0.708 0.2035 0.263)、(0.589 0.2495 0.295)、(0.6071 0.25 0.2978)、(0.7696 0.25 0.3114)和(0.8614 0.249 0.281); 选取大型车识别器的q为30(C=1)，识别中型车所用支持向量个数为4，分别为(0.975 0.2498 0.2704)、(0.894 0.23 0.332)、(1.198 0.248 0.3075)和(1.198 0.25 0.3647)。

2.4性能测试与结果分析

采用测试样本对三个识别器分别进行测试。测试样本由三种类型车辆数据组成，每类30个数据。测试分为识别器独立测试和分类器联合测试两部分。在识别器独立测试中，要考察每个识别器对本类数据的识别正确率和对其他类数据的识别正确率，独立测试结果见表3；进行联合测试即对3个分类器与表决器整体进行车型分类测试，测试依据为表2。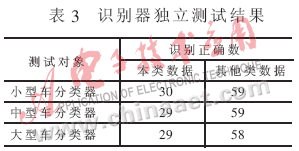


对表3中的测试结果进行分析，发现小型车识别正确率相当高,为98.89%；而中型车识别器和大型车识别器识别正确率分别为97.78%和96.67%。而且后两者对本类数据和其他数据均有错判现象发生。

由于本文设计的分类器采用了图1所示结构以及特殊的表决表(表2)，具有较强的容错能力，发生在小型车、中型车和大型车相邻类型之间的错判不会影响表决器的表决工作。只有当小型车识别器和大型车识别器均判为本类车时，表决器才输出“误判”。在联合测试时，分类器对90个测试样本的表决结果全部正确。

本文采用基于支持向量机的识别理论设计了一种可应用于不停车收费系统的车型自动分类器。该分类器与RFID(射频识别)技术相结合，能大幅度提升道路通行能力，有效打击各种作弊行为。