整数提升小波的算法分析及FPGA实现
小波变换是近几年发展起来的一门数学理论和工具.由于它具有良好的时频局部特性和多分辨率分析特性,因而在现代信号处理,特别是在图像数据压缩和处理中得到了广泛的应用.新一代静止图像压缩标准JPEG2000也将小波变换纳入标准之中,并采用二维离散小波变换(2D,DWT)作为系统编码算法的核心.
二维离散小波变换最有效的实现方法之一是采用Mallat算法,通过在图像的水平和垂直方向交替采用低通和高通滤波实现,如图1所示.这种传统的基于卷积的离散小波变换计算量大,计算复杂度高,对存储空间的要求高,不利于硬件实现.提升小波的出现有效地解决了这一问题.提升算法相对于Mallat算法而言,是一种更为快速有效的小波变换实现方法,被誉为第2代小波变换.它不依赖于傅立叶变换,继承了第1代小波的多分辨率特征,小波变换后的系数是整数,计算速度快,计算时无需额外的存储开销.Daubechies已经证明,任何离散小波变换或具有有限长滤波器的两阶滤波变换都可以被分解成为一系列简单的提升步骤,所有能够用Mallat算法实现的小波,都可以用提升算法来实现.

2 提升算法
对信号进行离散小波变换就是用多分辨率的形式分解信号,消除信号间的相关性。在每层分解信号都是用小波信号分解为高频段信号和低频段信号,即分别由相应的高通滤波器和低通滤波器来获得。提升方法是实现这些滤波运算的一个有效方法,而且方法相当简单。它使用基本的多项式插补来获取信号的高频分量,然后通过构建尺度函数来获取信号的低频分量。每一步提升包含个步骤分解,预测和更新.如图2所示.
分解
分解就是把信号at-1,分为偶数抽样点at,和奇数抽样点dt,这也称为懒小波变换(Lazy Wavelet Transform)。设信号at-1为有限长度的一维离散输入序列,它们之间存在一定的相关性。为了消除相关性,首选把信号at-1分解为两个子信号at和dt。一般来说,对于信号分解的形式、两个子信号的大小等,没有什么特别的限制,但要求存在某一与分解相对应的算子,可以从子信号at和dt,还原到at-1,这是离散小波变换和子带编码中最基本的要求,是由完全重构性质所决定的。在离散小波变换和子带编码中常用的是二通道向下抽样(Downsampling),也就是把信号at-1分解为偶数采样点at,和奇数抽样点dt。这个变换实际上什么也没做,对信号表示形式也没什么改进,但这是后面步骤的基础,所有的二进小波变换都是从这一步开始的。
预测
预测也被称对偶提升(Dual Lifting),就是由at预测dt,用预测误差代替dt,
dtdt-P(at)
at-1之间存在一定的相关性,故可以从at估计dt,令dt=P(at)这就是预测。也可以说,是将at作为at-1的近似值。若信号之间的相关性很大,那么预测效果会很好,将at作为at-1的近似表示不会“丢失”很多信息。这就意味着可以“扔掉”部分信息,即dt,以达到简练表示的目的。为了完全重建信号at-1,就只能“扔掉”包含在dt中的关于at的那部分信息,即可用dt-P(at)代替dt,既达到消除相关性的目的,也能保证存在某种逆算子,可以重建信号at-1。
更新
更新又称为主要提升(Primal Lifting),即用dt更新at,
atat+U(dt)
预测后得到的这样一种新的表示形式中,很可能会丢失信号的某些特征,如信号的均值,而这正是我们所期望的如对信号进行压缩时。为了恢复这些特征,在提升算法中又引入了另外一种操作一一更新(U),即用新得到的dt来更新at.
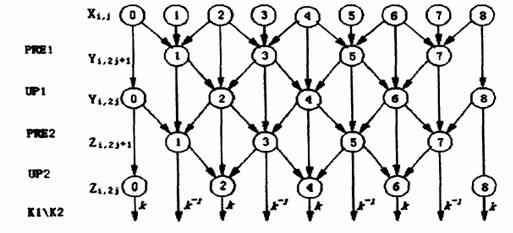
图3 提升算法的数据相关性
如图3所示,提升方法可以实现原位运算,即该算法不需要除了前级提升步骤的输出之外的数据,这样在每个点都可以用新的数据流替换旧的数据流.当重复使用原位提升滤波器组时,就获得了交织的小波变换系数.由于小波变换需要较大的计算量,且计算复杂度高,靠软件实现无法满足实用需要,其硬件实现日益受到重视.其中,基于FPGA的小波变换及编码方法一直是研究的热点.
3.算法分析
内存需求分析
对任何设计来说,我们都希望所耗的内存越小越好。针对这点,在整数小波变换的设计中,首先要考虑到的就是整数小波系数的动态范围,因为它直接决定内部存储器的字宽,在存储器数量一定的情况下也就决定了所有存储器的容量。
以整数5/3小波变换为例,设输入信号为8位无符号数。那么沿行进行计算时,最大的可能值为255,最小可能值为-255,故细节值d的最坏状态必须用S9(表示9位有符号数.对一个J级分解的小波变换来说,为了能一致的表示所有小波系数,内部存储器字的位宽必须满足最坏的情况(就是在第J级的字长),这个字长就是S(8+2J)。例如,个J=4级的分解需要S16来表示得到的小波系数。
边界延拓处理
小波变换中,必须对原始图像分块边界数据进行对称周期性延拓。设有信号ABCDEFGH,则延拓过程 如图4所示

图4 对称周期数据延拓过程
如果将对原始图像边界数据的对称周期延拓作为单独的模块独立于小波变换模块之外,将增加存储器的数量和读写操作,增大硬件的面积。因此文献[1]提出了一种将对称周期延拓与小波变换模块完全结合在一起的针对5/3小波变换的算法,文献[2]又对该算法进行了一定的改进,使该算法在硬件实现时有更低的计算复杂度。该算法采用分段函数表示,用以将边界延拓过程内嵌于小波变换模块中,分为3个阶段:1)起始阶段, 2)长时间的正常运行阶段,中间数据的处理;3)结束阶段,处理右端数据,奇、偶数序号信号结束分别。
算法改进
针对上面的改进算法[2],我们设计了一个5/3小波变换FPGA硬件结构,如图5。将预测系数改为正,预测部分加改为减,采取直接运算,降低运算复杂度;采取增加控制状态,复用正常计算时的硬件结构。很明显,这种改进的“内嵌延拓提升小波变换”FPGA硬件结构与文献[1]比较,每行(每列)减少二个额外的硬件运算模块,降低了计算复杂度。对图像的小波压缩处理来说,提高了运算速度和硬件芯片的利用率,同时降低功耗。
4.FPGA实现
根据以上的论述,我们设计以如下的实现方案,如图5所示。
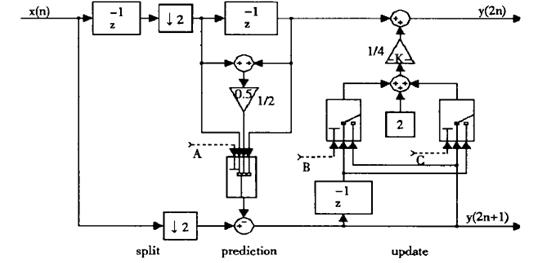
5 性能分析
我们采用FPGA为Xilinx公司生产的 Virtex2-Pro 系列XC2VP30,所需要的资源如表1所示。
表1 整数小波变换占用FPGA资源

6 展望
如果采用更高系列的FPGA芯片, 无疑会达到更高的处理速度,但性价比是工程中考虑的一个重要因素。随着FPGA内部集成了越多越多的功能,用FPGA实现复杂运算会受到人们越来越多的青睐。






评论