基于新型CMAC控制方法的电动加载系统
摘要 在电动加载系统中,多余力矩强扰动和其他非线性因素直接影响力矩跟踪精度,传统的控制方法难以得到满意的控制效果。文中分析了传统CMAC算法不稳定的原因,提出了一种新型CMAC控制策略,并对其结构及算法进行了研究。在控制结构上以系统的指令输入和实际输出作为CMAC的激励信号,采用误差作为训练信号,并根据激励信号的特点,提出了非均匀量化的思想。动态仿真结果表明,该方法有效抑制了加载系统的多余力矩及摩擦等非线性因素干扰,提高了电动加载系统的控制精度,且增强了系统的稳定性。
本文引用地址:http://www.amcfsurvey.com/article/201610/306604.htm电动负载模拟器是典型的被动式加载系统,存在着由被加载系统主动运动引起的多余力矩。多余力矩的存在会严重影响加载系统的控制精度,因此如何抑制乃至消除多余力矩是电动负载模拟器必须解决的关键问题。传统的控制方法有结构不变性原理和同步补偿等,这些方法需要相对精确的数学模型,但在实际的电动负载模拟器中,存在非线性(如摩擦、机械连接间隙等)以及参数变化问题,通常达不到理想效果。CMAC(Cerebellar Model Articulation Controller)神经网络,具有学习速度快、对学习数据出现次序不敏感、不存在局部极优,结构简单易于软硬件实现等优点,被广泛应用于神经网络建模、控制、模式识别等领域。目前常用的是Miller等人提出的CMAC和PD的复合控制策略,这种控制结构在跟踪阶跃输入或方波信号时,具有输出误差小、实时性好、鲁棒性强等特点,但在跟踪连续变化信号如正弦波时,会因累积误差的影响产生过学习现象,进而导致系统的不稳定,稳定性问题是控制系统得以实现的前提条件,本文对CMAC复合控制算法进行了研究和改进,提出了一种新型基于最优权值法的CMAC复合控制策略,改进后的控制算法在保证系统稳定性的前提下,提高了动态特性和跟踪精度,适合于实时控制,仿真结果证明了该算法的有效性。
1 常规CMAC复合控制分析
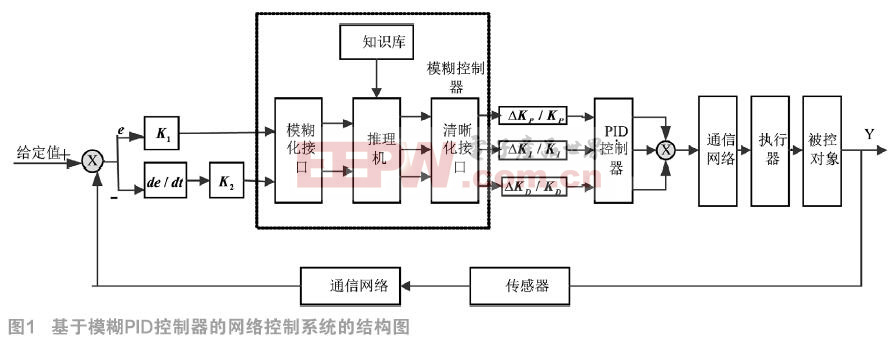
目前常用的CMAC和PD复合控制器结构如图1所示。
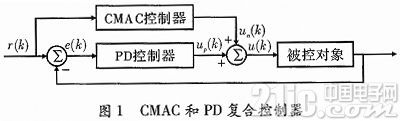
1.1 CMAC误差校正值分配分析
常规CMAC误差的校正值被平均地分配给所有激活存储单元,并未考虑这些存储单元的可信度。这种权值更新算法违背信度分配的概念,降低了 CMAC的收敛速度,实际更新的效果应该与激活存储单元的可信度成比例。权值调整的过程,本质上反映了网络“学习”与“遗忘”的关系,学习次数越多,存储的知识越多,可信度越高,权值改变越少,因此在网络权值的调整过程中,必须考虑“新知识学习”和“旧知识遗忘”的平衡问题。
1.2 稳定性分析
1.2.1 CMAC算法不稳定原因分析
针对无人机舵机电动负载模拟器的控制需求,采用常规CMAC和PD复合控制解决模拟器的转矩控制问题,以文献中的电动负载模拟器模型为基础进行仿真,采样时间取0.001 s。本文中加载指令设为rin=10 sin(2πk/100)N·m。取CMAC量化级数N=100,泛化常数C=10,学习率η=0.05,不考虑多余力矩影响,控制结果如图2(a)所示,其中横坐标表示仿真周期数,仿真周期等同于加载指令周期,每个周期包含100次仿真,纵坐标表示每个仿真周期的最大误差,控制系统明显不稳定;另外为了验证CMAC和PD相互作用对稳定性的影响,单独对CMAC控制进行仿真分析,控制结果如图2(b)所示。为验证加载指令信号幅值、频率对稳定性的影响,分别对加载指令取不同幅值和频率进行仿真,仿真结果如图3所示。对比图3(a)、图3(b)及图2可看出,指令信号的幅值影响了跟踪误差的大小,但对控制系统发散快慢的影响不明显。对比图3(e)、图3(d)及图2可看出,随着指令信号频率的增加,控制系统的跟踪误差变大,发散变快。
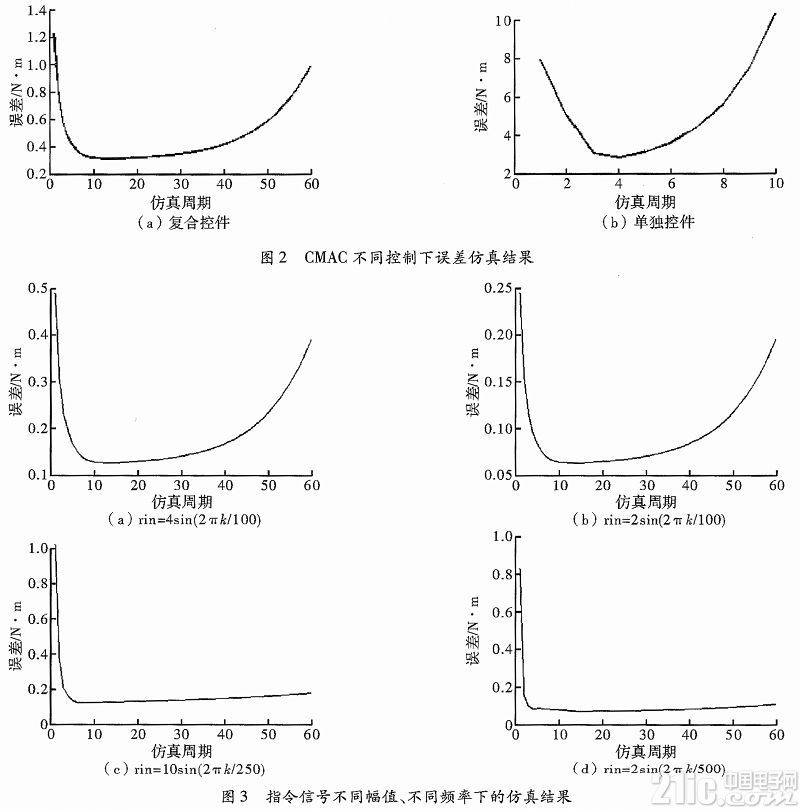
对比图2和图3可知,CMAC+PD复合控制和单独CMAC控制时误差变化趋势是一致的,即开始阶段算法都能起到控制作用,但随着误差的累积会产生过学习现象,进而导致系统发散。因此,排除了CMAC和PD相互作用引起不稳定的可能性,算法不稳定的原因应在CMAC本身。由图2和图3还可以看出,PD算法的加入确实能在一定程度上增强系统的稳定性,加快系统的收敛速度。CMAC算法的工作过程包括概念映射、实际映射、输出算法以及学习算法。分析可得影响 CMAC控制结果的主要因素是参数以及权值更新算法。
1.2.2 CMAC算法稳定性基础分析
影响CMAC控制结果的参数有泛化常数C,量化级数N和学习率η,下面分别研究其对控制结果的影响。
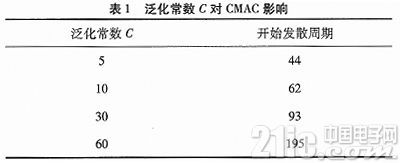
(1)泛化常数C。
由表1可知,随着泛化常数C的增大,可在一定程度上增强系统的稳定性,延长稳定时间,但是最终仍会发散,并随着泛化常数的增大,算法的运行时间也会相应变长。
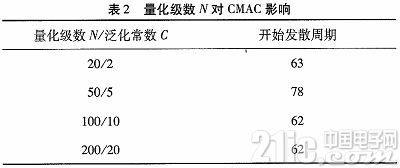
(2)量化级数N。
为了减小泛化常数的影响,在此实验中对不同的量化级数保证相同的量化区间重叠率。
由表2可知,量化级数只要选取合适即可,当量化级数大于某一值时,系统稳定时间并没有太大变化。
(3)学习率η。
由表3可知,学习率越小,系统稳定的时间越长,学习率越大,系统稳定的时问越短,当学习率大于某一值时,系统直接发散。但是减小学习率只能在一定程度上延长稳定的时间,并不能从根本上解决不稳定问题,且过小的学习率会导致系统的快速性变差。

综上所述,改变CMAC的参数只能在一定程度上延长系统的稳定时间,但不能从根本上解决不稳定的问题,解决不稳定问题必须从其他方面着手。
2 改进的CMAC算法
由图3可知,系统误差是按先收敛再发散的趋势进行。即开始阶段,控制算法能对误差起到控制作用,但当误差收敛到某一值后,由于误差的累积而产生过学习现象,从而导致系统开始发散。基于此,本文提出了一种新的权值更新方法——最优权值法。如式(1)所示

即当开始阶段误差减小,控制算法正常学习时,采用公式wj(t)=wj(t-1)+△wj(t)进行权值的更新,进行正常的学习过程,此时权值为增量式更新;当算法开始过学习,即系统误差开始由小变大时,将此时的权值wj取为最优权值wbest,采用公式wj(t)=wbest+△wj(t)进行更新,此时,权值为原地式更新,这样一方面可避免过学习现象,另一方面又可对误差进行及时的响应。如果在电动加载的过程中,加载指令或者加载对象运动发生突然改变,导致加载误差超过指标要求,权值更新重新进入增量式更新阶段,当权值变为最优值时,进入原地式更新阶段,从而保证加载过程中的精度和稳定性。
3 仿真及结果分析
对电动负载模拟器模型,采用如图4所示的改进的CMAC和PD复合控制结构。

其中,PD参数设定为Kp=2,Kd=0.005;CMAC的参数设定为:N=100,C=15,η=0.2,α=0.2,k=1.3。下面分别对改进的CMAC+PD控制算法以及传统CMAC+PD复合控制算法进行仿真分析。
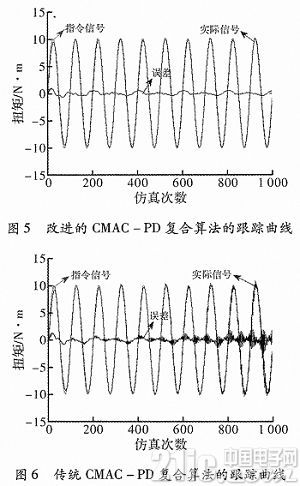
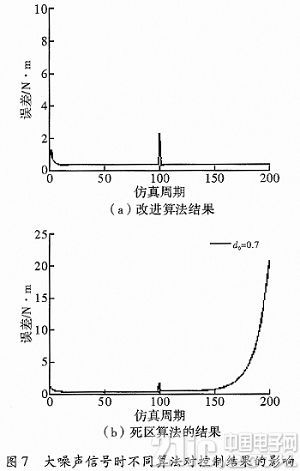
同样,加载指令为rin=10 sin(2πk/100)N·m,加入多余力矩影响,角速度干扰信号设为rin=1.74sin(5×2π×t)。图5为改进后的CMAC+PD复合方法的跟踪曲线,误差可收敛到0.314 9。图6为传统CMAC+PD复合方法的跟踪曲线,误差可收敛到0.527 4,在1 000次时已出现发散趋势。为了检测改进算法和文献死区算法的稳定性,在第100个仿真周期,对两种算法忽然进入一个幅值为2 nm的大噪声信号,如图7所示,死区算法最终发散;而改进算法,系统仍然保持稳定,具有较强的鲁棒性。
4 结束语
本文针对飞机电动负载模拟器的控制需求,对CMAC和PD复合控制策略在误差校正值分配、跟踪连续变化信号时的不稳定现象进行了研究和分析,提出了一种基于最优权值法的新型CMAC控制算法,即当CMAC算法正常学习时,权值正常更新,当CMAC算法过学习时,具有较高的稳定性。仿真表明,相比于传统CMAC和PD的复合控制策略,改进的CMAC和PD复合控制策略既可保证系统的稳定性又可保证系统的跟踪精度,既能及时响应误差且又具有较强的鲁棒性,适合于非线性系统的实时控制。






评论