基于FPGA的Alpha半透明图像叠加算法硬件实现
摘要:文中在FPGA上采用纯verilog逻辑实现了Alpha半透明图像叠加算法,即验证了算法的正确性,同时针对FPGA不善于处理浮点运算的弊端,采用了移位操作的方法,进一步提高了运算速度,实现了Alpha透明系数可调,半透明图像叠加的实时显示,在高清图像显示领域具有很大的实用价值。
本文引用地址:http://www.amcfsurvey.com/article/201609/303572.htmAlpha透明算法被广泛应用于图像处理,2D游戏,3D游戏图像混合和渲染等领域。在涉及到高清图像时由于计算量比较大,PC处理速度较慢,图像半透明叠加效果无法实时呈现。本文采用了FPGA并行处理的思想,同时对逻辑中设计到的浮点运算进行了移位操作,极大的提高了运算速度,实现了图像的半透明叠加效果的实时显示。可以在高清图像显示领域中实现视频和半透明滚动字幕的叠加,以及多路视频的实时叠加处理。
1 Alpha算法
Alpha通道是一个8位的灰度通道,该通道用256灰度来记录图像中透明度信息、定义透明、不透明和半透明区域,其中黑表示全透明,白表示不透明,灰表示半透明。
Alpha混合算法公式:

R(A)、G(A)、B(A)分别代表图像A的RGB分量的原色值,R(B)、G(B)、B(B)分别代表图像B的RGB分量的原色值,R(C)、G(C)、B(C)分别代表混合后图像C的RGB分量的原色值。
alpha为图像的透明度系数,取值为0—1,1为完全透明,0为完全不透明,改变这个值可以得到一个渐变的效果。
透明度alpha的计算。颜色在本质地上是光的产物,可以把透明度理解为玻璃的透光性。例如一个alpha=0.2的颜色,可以将其想象为透光率为80%的彩色玻璃。透过这块玻璃看去,由于80%的光都透过了,因此留下来的颜色只剩20%,即所谓系数为0.2的alpha。
2 Matlab验证效果
现在通过Matlab来进行两幅图片叠加验证。
将alpha设为0.4和0.6的颜色进行叠加。这时相当于叠加了两块玻璃,一块透光率为60%,另一块为40%。一道光束穿过,经过60%透光率玻璃时,光线强度剩下80%,再经过40%透光率玻璃时,光线进一步被削弱,只剩下60%*40%=24%。这意味着合成的图片有24%的透明性。
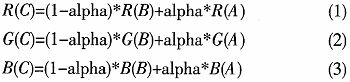
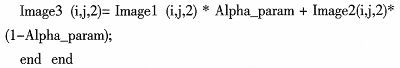
两幅图片的分辨率都是1 024*768,叠加后处理效果图如下:
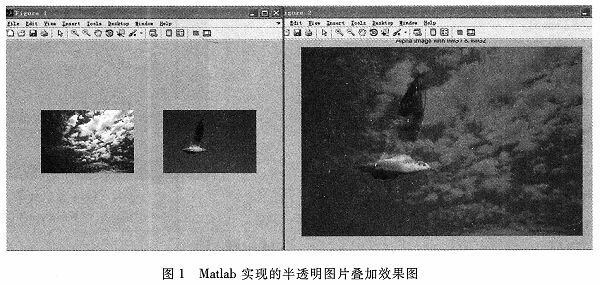
由效果图可以看出,实现了海鸥在蓝天白云中飞翔的半透明效果。由于蓝天白云图片alpha为0.4,海鸥图片alpha为0.6,所以海鸥透明度明显高于蓝天白云。随着蓝天白云alpha值的提高,透明度也会提升,相反海鸥透明度会随之降低。
虽然实现了半透明叠加效果,但由于图片分辨率过高,Matlab要对每个像素点的RGB三通道分别进行alpha算法公式运算,最后输出合成图片,用了大约0.75 s的时间。对视频图像无法做到实时处理的效果。因此,考虑用FPGA硬件设计来实现此算法。
3 FPGA硬件实现
本设计硬件采用的市面上常用的开发板,主控芯片是ALTERA公司的Cycelone IV,并带有VGA,百兆网口,RS232串口等一系列接口。FPGA内部产生两幅图片同时进行半透明化叠加,并且通过开发板上的按键来控制alpha系数,从而实现调节两幅图片的之间的透明度,最后在VGA显示器进行显示。
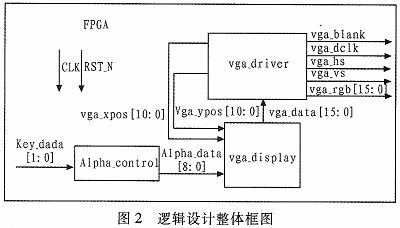
3.1 逻辑设计整体框图
整体框图包括3个模块,alpha_control模块、vga_display模块和vga_driver模块
alpha_control模块:通过外部按键控制alpha半透明参数,实现两幅叠加图片之间透明度实时转换。
vga_display模块:由于FPGA内部的memory容量有限,无法存储高分辨图片,因此通过此模块生成两幅图片,并实现半透明图片的叠加,然后送到VGA显示器进行实时显示。
vga_driver模块:驱动VGA[5]工作在预定的分辨率下,这里驱动显示器工作在1024*768@65MHz的分辨率下。
3.2 VGA驱动原理
VGA驱动本质就是在一定工作频率下,产生准确的时序关系包括:VS-垂直同步信号,HS-水平同步信号,消隐信号之间的关系。
在VGA显示过程中,完成一行扫描所要的时间为水平扫描时间,完成一帧扫描所需要的时间称为垂直扫描时间。每扫描完一行用行同步信号进行同步;扫描完所有行后用场同步信号进行同步。本文设计采用的是1024*768@65MHz模式。依据时序标准,每显示行包含1344个点,其中1024为显示有效区,320点为消隐区,每行的行同步脉冲低电平宽度为136个像素点;同理每场有806行,有效行为768,其中场同步脉冲低电平宽度为6行。
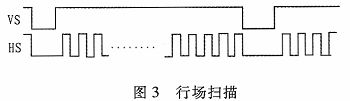
如上图所示,每一场的扫描都包含若干个行扫描,如此往复循环。
3.3 Alpha算法verilog实现
为了实现快速运算,这里将透明比例按2的N次幂来分级(Alpha=1/256),同时进行了移位算法,式(1)、式(2)、式(3)变为以下公式:
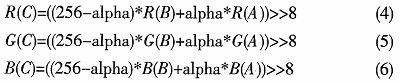









评论