基于数字图像处理技术的岩石节理宽度测量

2 图例应用
2.1 岩石节理图片的采集
　　首先，获取岩石标本。对需要研究的岩体进行钻孔，并向孔中放入放射性物质，经过一个星期的放射过程使放射物充满岩体中可以达到的裂隙。然后，切割岩石。用10～50倍显微镜采集有代表性的节理的原始彩色图像。本例中采集样本使用的放大比例设定为：一个光点代表的实际长度为0.004mm。由于选用了比较大的放大比例，使微节理裂隙的物理特征更加突出，图片规模也随之较大。采集过程中把整条节理裂隙分成34张独立图像分别拍摄，每张图片的大小为760×230个象素点。为简洁起见，文中选取该组图片中的一张进行处理并对各种测量方法和结果进行对比分析。
2.2 图像处理过程
　　首先对采集到的原始彩色图像进行二值化处理， 为便于各种算法的测量比较以及减少偶然性误差，对被分析的图像采取平均分割的方法等分成7份，对分割后的图像使用改进的Ferret算法进行测量。图3和图4为裂隙的原始图和二值化后被分割的图像。此裂隙变化较复杂，起伏较大，裂隙中间有孔洞(或填充物质)，边界有“烟雾”，这些都会影响测量的准确度，因此测量前先采用阈值法去除边界噪声。经过改进的Ferret算法处理后的效果图如图5所示，测量结果统计如表１所示。

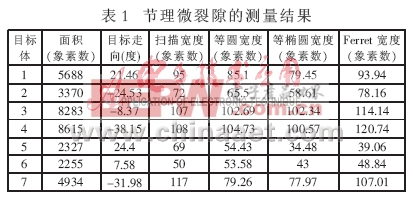
2.3 统计分析
　　由于椭圆算法使用广泛且结果理想，所以以它作为基准进行对比分析。三种算法宽度测量结果的对比如图6所示。由图可知：对于3、4、7这三段的测量，当量圆直径算法和椭圆算法得出的结果比较接近，从图4中也可以看出3、4、7各段裂隙的长宽差值近似。在这种情况下Ferret算法并不能表现出很好的优越性；而对于5、6段的测量，椭圆算法和Ferret算法的结果比较接近，但5、6二段的长宽差很大，可见对于长宽差比较大的不规则图形可以使用Ferret算法测量。这就要求使用Ferret算法进行实际测量时，要注意测量前的分割尺度，使长宽有一定的差距，使用Ferret算法才可以达到理想的效果。
　　经过大量宽度测量的实验对比表明：Ferret算法在测量不规则图形，特别是那些长宽差比较大的图形都得到了理想效果。
3 总 结
　　大量的数字图像处理技术应用在工程测量方面，由于其各异性，面对众多测量算法，要选用某种适合的算法，需要做大量的对比研究。对于规则的被测图形来说，当量圆算法和当量椭圆算法基本可以满足需求，而Ferret算法在大量长宽差比较大的不规则图形测量方面表现出良好的适应性，而且达到了满意的效果。本文分析了简单Ferret算法的原理，提出了改进的Ferret算法，给出了一个基于改进的Ferret算法的岩石节理宽度测量的实例过程。然而，在实际测量中，分割图像时选取的长度大小、非实裂隙的中间孔洞以及边界噪声等都会对宽度测量产生一定的影响，这些都将是今后要解决的问题。