赫夫曼编译码系统的设计与实现

摘要：在信息快速传输和存储过程中，数据压缩有着重要的作用。从赫夫曼树定义及算法出发，介绍了一个赫夫曼编译码系统的设计与实现过程。这对于深入理解数据结构、程序设计有益。
关键词：赫夫曼树；赫夫曼编码；赫夫曼译码

在数据结构课程的实践环节中，通常会让学生利用赫夫曼编码进行文本压缩与解压缩。由于教材上只是给出了赫夫曼树的定义及算法，学生会感到无从下手。本文将从赫夫曼树定义及算法出发，通过实例介绍赫夫曼编译码系统的具体设计与实现过程。

1 设计内容
1．1 赫夫曼编译码系统功能模块
(1)赫夫曼建树模块：根据输入的字符和频率，完成赫夫曼树的构造，并根据赫夫曼树求赫夫曼编码。
(2)编码模块：读取文本文件进行编码，编码结果存入到新文件。
(3)译码模块：读取编码文件并解码，打开存储编码的文件，根据所读取的编码文件中的每个字符，利用赫夫曼树进行解码。
(4)输出模块：将解码后的每个字母写入到一个新的文件中。
1．2 测试数据
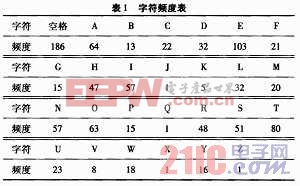
用表1给出的字符集和频度的实际统计数据建立赫夫曼树，并实现以下报文的编码和译码：“THISPROGRAM IS MY FAVORITE”。

设计调试环境为Microsoft Visual C++6．0系统。

2 设计原理及算法分析
本次要做的赫夫曼编译码系统的主要功能是：运用二叉树来设计二进制的前缀编码。给一个文件，先统计文件中每个字符出现的频数，即作为此字符的权值，然后将里面的字符编码成相应的赫夫曼编码。最后，根据赫夫曼译码原理把所给二进制数编译成对应的字符串。
2．1 构建赫夫曼树
一般而言，给定n个实数w1，w2，…，w3其中，n≥2，求一个具有n个结点的二叉数，使其带权路径长度最小。可以证明赫夫曼树的带权路径长度是最小的。
(1)根据与n个权值|w1，w2，…，w3|对应的n个结点构成具有n棵二叉树的森林F={HT1，HT2，…，HTn}，其中第i棵二叉树HTi(1≤i≤n)都只有一个权值为wi的根结点，其左、右子树均为空。
(2)在森林F中选出两棵根结点权值最小的树作为一棵新树的左、右子树，且置新树的根结点的权值为其左、右子树上根结点权值之和。
(3)从F中删除构成新树的那两棵，同时把新树加入F中。
(4)重复第1和第3步，直到F中只含有一棵为止，此树便为赫夫曼树。
2．2 赫夫曼编码
赫夫曼编码是根据可变长最佳编码定理，应用赫夫曼算法而产生的一种编码，是消除编码冗余度最常用的方法。它的平均码字长度在具有相同输入概率集合的前提下，比其它任何一种可译码都小，因此，也常被称为紧凑码。
(1)给定字符集的赫夫曼树生成后，求赫夫曼编码的具体实现过程是：依次以叶子HT[i](0≤i≤n-1)为出发点，向上回溯至根为止。上溯时走左孩子则生成代码0，走右孩子则生成代码1。
(2)统计从根到叶子的路径上的标号依次相连，便为该叶子所对应字符的编码。
(3)用生成的各个字符的编码替代原文件中的相应的字符，生成decode．txt文件。