基于FPGA的高阶QAM调制器的实现

　　1 引 言

　　多电平正交幅度调制MQAM(Multilevel QuadratureAmplitude Modulation)是一种振幅和相位相结合的高阶调制方式，具有较高的频带利用率和较好的功率利用率。因为单独使甩振幅和相位携带信息时，不能最充分利用信号平面，这可由调制信号星座图中信号矢量端点的分布直观观察到。多进制振幅键控(MASK)调制时，矢量端点在一条轴上分布；多进制相位键控(MPSK)调制时，矢量点在一个圆上分布。随着进制数M的增大，这些矢量端点之间的最小距离也随之减少。而MQAM采用振幅和相位联合键控调制，他能充分利用整个信号平面，将矢量端点重新合理地分布，在不减小最小距离的情况下，增加信号的端点数；在相同信号端点数的情况下，矢量端点之间的最小距离增加。因此，MQAM是一种高效的调制方式，被广泛应用于中、大容量数字微波通信系统、有线电视网络高数据传输、卫星通信等领域。本文首先介绍了MQAM调制解调的基本原理，然后以64QAM为例，介绍了一种全数字实现的调制系统结构方案，并给出了解调器的具体FPGA实现方法及关键技术。

　　2 MQAM调制原理

　　所谓正交振幅调制，就是用两个独立的基带波形对两个相互正交的同频载波进行抑制载波的双边带调制，利用这种已调信号在同一带宽内频谱的正交性来实现两路并行的数字信息传输。MQAM信号的一般表达式为：

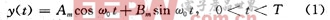
　　式(1)由两个相互正交的载波构成，每个载波被一组离散的振幅{Am)，{Bm)所调制，故称这种调制方式为正交振幅 调制。式中T为码元宽度，m=1，2，…，L，L为Am和Bm的电平数。MQAM中Am和Bm振幅可以表示成：

　式中：A是固定的振幅，dm，em由输入数据确定，dm，em决定了已调MQAM信号在信号空间中的坐标点。在调制过程中，载波的振幅与相位都发生了变化，因此，已调信号矢量星座图中每一个坐标点代表了一种编码组合，同时也代表了正交信号矢量合成后的不同的相位及电平，第i个信号可用数学描述为：

　　因此每一个坐标点也由Ai和φ i惟一确定。

　　3 64QAM调制器系统设计

　　图1给出了全数字实现的64QAM调制器的电路原理结构。除D／A变换外，每个功能模块都用FPGA实现。扰码、串并转换和差分编码采用原理图的方法进行设计，电平转换及星座图映射采用查表法(LUT)进行设计。本设计的难点为成形滤波器和基于DDS的正交调制器实现，下面重点描述成形滤波器和基于DDS的正交调制器的实现方法。

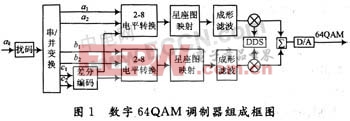
　　3.1 成形滤波器的设计

　　为了让信号在带限的信道中传输，提高频谱利用率，通常在发送端把信号经过成形滤波器进行带限，由此就会引入码间干扰。为有效地减少码间干扰，按照最佳接收理论，收发基带滤波器应共轭匹配，设计时收发基带滤波器采用均方根升余弦滚降滤波器即能满足要求。

　　在实际电路设计中采用具有线性相位的FIR滤波器来实现均方根升余弦滚降特性的成形滤波器。一个N阶FIR滤波器的差分方程表达式为：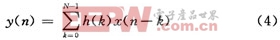

　　线性相位的FIR滤波器的系数是偶对称或奇对称的，利用系数的对称性可减少乘法器的数量，本系统采用N为偶数且系数偶对称的线性相位的FIR滤波器。滤波器系数是一个固定的值，根据均方根升余弦的冲击响应特性，利用Matlab软件可直接生成FIR数字滤波器系数hk(k=0，1，…，N-1)。所以滤波器的乘法都是固定系数的乘法。