基于FPGA的LDPC编码设计
1 LDPC码
LDPC码是一种线性分组码,其校验矩阵是稀疏矩阵,因为相应的校验矩阵中包含绝大多数的0而仅有极少数的1而得名。一个(n,k)二进制LDPC码可以用一个非常稀疏的奇偶校验矩阵H来表示。其中,H是一个mxn的矩阵,n表示编码比特长度,m表示校验比特长度,k=n-m是信息比特长度。与校验矩阵H相对应的是一个生成矩阵G,生成矩阵将要发送的信息s={sl,s2,…,sm}转换成被传输的码子c={c1,c2,…,cn},n>m。对于任何一个合法的码字c,都有校验方程HcT=0。
2 RU编码算法
LDPC码属于线性分组码。信号通过LDPC编码后的码字符合公式:

式中,c为码字,H为校验矩阵。
直接的编码方案:1)高斯消元,将校验矩阵H化为下三角形式:2)将c分为信息比特和校验比特2部分,如x=(s,p),其中s为已知信息比特向量,p为待求校验信息比特向量;3)利用前向迭代方法解方程HcT=O,得到p。由于高斯消元后的矩阵不再具有稀疏性,因此这种编码方法的硬件实现方案,其复杂度是与码长的平方成正比。为了降低复杂度,Richardson和Urbanke充分利用校验矩阵的稀疏性,将LDPC码的编码复杂度降到与码长n成线性关系,即RU算法。
RU算法包括两个阶段:预处理阶段和信号编码阶段。通过预处理将校验矩阵日变为一个近似下三角的矩阵,由于这种变换仅仅通过行置换来实现,所以矩阵的稀疏特性被保留。如图1所示,在校验矩阵H的近似下三角形式中,分块矩阵A、B、C和c都保持了稀疏性,D为密集矩阵,T为稀疏的下三角矩阵。当g很小时,即矩阵D很小时,可以大大降低编码运算复杂度。为减少运算量应在设计H矩阵时使g越小越好。
实际编码由矩阵相乘、前向迭代和向量相加操作组成。对于给定的一个校验矩阵,预处理编码预处理过程和矩阵的计算只需要做一次,所以可先用软件完成,实际编码在硬件上完成。RU编码算法中可以进行部分并行运算,使得吞吐率最大化。通过有效的矩阵存储,降低存储单元的消耗量。
2.1 编码器设计
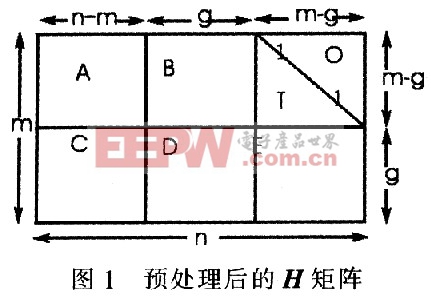
预处理包括2步:三角化和秩校验。三角化通过行列置换处理将校验矩阵转化成图1所示的形式,则:

式中,A为(m-g)×(n-m),B为(m-g)×g,T为(m-g)×(m-g),C为gx(n-m),D为gxg,E为gx(m-g)。除D外,其他全是稀疏矩阵,且T为对角线上全为l的下三角矩阵。









评论