一种高效咬尾卷积码译码器的设计与仿真
摘要:介绍了咬尾卷积码的最优和次最优译码算法的实现细节。给出了采用新的蝶形图计算方法和环形内存来节省硬件资源的实现方法,最后给出了次最优算法在FPGA上的实现结果。
关键词:咬尾卷积码;次最优译码算法;蝶形图;FPGA
0 引言
自1955年Elias发明卷积码以来,卷积码作为一种高效的信道编码已被用在许多现代通信系统中。卷积码分为零比特卷积码(Zero Tail CC,简称ZTCC)和咬尾卷积码(Tail Biting CC,简称TBCC)两种。ZTCC是指在编码的时候,码字后面要另外加上K(K为约束长度)个0将编码寄存器的最后状态打出,而TBCC则是直接用码字的最后K个比特将编码寄存器初始化,从而提高编码率。现在的3G和4G通信标准中(比如WiMAX或LTE)都采用了TBCC信道编码。关于TBCC的译码算法很多,其中比较经典的译码算法有循环维特比算法(CVA)和BCJR算法。但上述算法由于解码时延不固定和复杂度的原因,均不便于硬件实现。为此,本文提出了一种便于硬件实现的次优解码算法。
1 TBCC译码算法
1.1 最优译码算法
TBCC的理论最优译码算法是,对于每一个可能的初始状态(3k)用维特比译码算法对所有可能的状态进行搜索,最后再根据最好的状态进行解码。但是,这种算法的复杂度太高,不利于硬件实现。
1.2 次最优译码算法
次最优译码算法的经典代表是CVA算法,此外还有其改进的算法比如环绕维特比算法(WAVA)和双向维特比算法(BVA)。它们的主要思路是利用圆形buffer将码字扩展成多个相同码块首尾相接的长码块进行译码。当检测到首尾状态相等或者满足自适应迭代的停止条件时,即完成译码;否则继续进行迭代。但该算法或其改进的WAVA和BVA算法都存在这样一个问题。那就是解码的延迟不是固定的,而这非常不便于硬件实现。
所以,本文中提出固定延迟的译码算法,其基本思路是在码块的前Lt个符号补在符号的后面,将码块的后Lh个符号补在码字的前面,这样就构成一个长度为Lt+N+Lh的新码块(假设原码字长度为N),图1所示是重构的码块示意图。该新码块可以按照ZTCC解码一样去解码,然后从具有最小路径度量(path metric)的状态进行回溯。
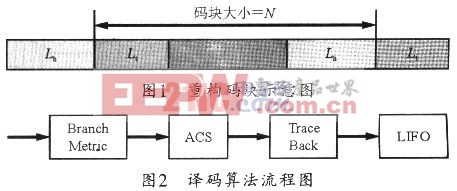
图2所示是其译码算法流程图。其中Lt和Lh参数的选择应根据仿真来确定。这里采用典型值:Lt=72,Lh=96。









评论