基于FPGA的自适应波束形成算法实现

　1 引 言

　　在雷达及声纳信号处理系统中，波束形成算法通常采用DSP软件编程实现，控制逻辑电路采用CPLD来完成，这种方法具有软件编程灵活、功能易于扩展的优点，但对于实时性能要求很高的系统，如雷达、声纳探测和超声成像等系统中为了提高对目标变化实时跟踪和测量，就必须尽量缩短信号处理的时间，过长的运算处理时间会对水下目标的探测性能产生较大的影响。声纳的检测能力就会迅速下降，以至完全失去检测能力，而自适应波束形成技术（ABF）就是声纳能够根据周围环境噪声场的变化，不断地自动调节本身的参数以适应周围环境，抑制干扰并检出有用信号。因此采用FPGA来实现自适应波束形成算法是满足复杂海洋环境超声阵列波束形成的较好途径。

　　最小均方自适应算法（Least Mean Square，LMS）较其他自适应算法具有结构简单，计算量小，易于实现等特点。FPGA实现LMS自适应波束形成算法比采用现有DSP来实现可以明显提高信号的处理速度，节约资源，能更好地满足复杂多变的海洋环境，具有广泛的实用价值。

　　波束形成系统相当于一个时空滤波器，自适应波束形成系统可采用IIR和FIR两种结构。与IIR滤波器相比，FIR滤波器具有以下优点：可得到严格的线性相位；主要采用非递归结构，从理论上以及从实际的有限精度运算中，都是稳定的；由于冲激响应是有限长度的，因此可以用快速傅里叶变换算法，运算速度快；FIR滤波器设计方法灵活。

　　本文采用自适应的FIR滤波器结构，结合时延最小均方（DLMS）算法，充分利用FPGA芯片运算速度快，存储资源丰富等优点设计和实现了基于FIR超声阵列自适应波束形成。主动声纳信号为窄带信号，通常采用复数形式表示，在空间滤波器模块采用了循环移位流水乘加器，使复数乘加运算节约了大量资源，同时用并行乘法器完成了DLMS算法，并给出了系统软、硬件模块和仿真分析。

　　2 超声阵列波束形成系统模型及原理

　　2.1 系统架构及原理

　　自适应波束形成又称自适应空域滤波，他是通过对各阵元加权进行空域滤波，来达到增强有用信号、抑制干扰的目的，而且他可以根据信号环境的变化，来改变各阵元的加权因子。在理想的条件下，自适应波束形成技术可以有效地抑制干扰而保留期望（有用）信号，从而使阵列的输出信号干扰噪声比（SINR）达到最大。自适应过程的实现可以采用任何一种适用于横向结构滤波器的自适应迭代算法，比如Wiener滤波器，或者最小均方（LMS）算法。本设计采用最小均方（LMS）算法，系统结构原理如图1所示。

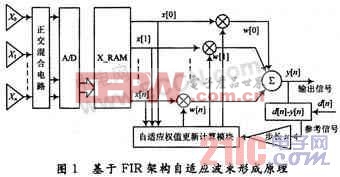
　　基于FIR自适应波束形成系统过程如下：一方面，输入信号与表示在n时刻的值可调节权系数ω1（n），ω2（n），…，ωm（n）相乘后相加得到输出；另一方面，将输出信号与期望信号进行对比，所得的误差值通过一定的DLMS自适应控制算法再用来调整权值，以保证空间滤波器处在最佳状态，实现滤波的目的。

　　FIR由线性系统理论可知，在某种适度条件下，输入到线性系统的一个冲击完全可以表征系统。当我们处理有限的离散数据时，线形系统的响应（包括对冲击的响应）也是有限的。若线性系统仅是一个空间滤波器，则通过简单地观察它对冲击的响应，我们就可以完全确定该滤波器。通过这种方式确定的滤波器称为有限冲击响应（FIR）滤波器。

　　FIR滤波器是在数字信号处理（DSP）中经常使用的两种基本的滤波器之一，另一个为IIR滤波器。IIR滤波器是无限冲激响应滤波器。

　　在延时LMS算法（the Delayed LMS Algoritms，DLMS）中，将系数更新延迟几个采样周期，只要延迟小于系统阶数，也就是滤波器长度，则误差梯度[n]=e[n]x[n]，也就是[n]≈[n-D]，但对于由FPGA实现的乘法器和系数更新需要额外的流水线级，如果引入一个延迟因子D，μ为步长因子，LMS算法就变成：