普通点对点布线技术分析

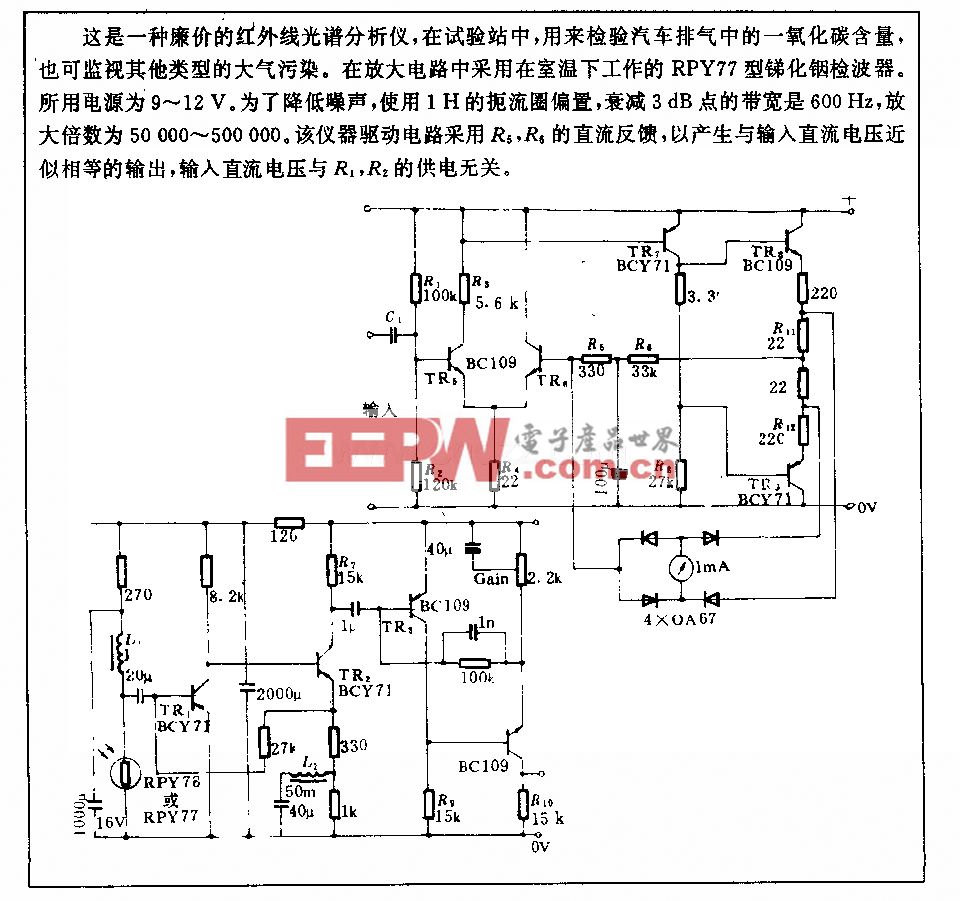
最近，硅谷有一定著名的公司，我们称之为NEWCO公司，曾经制造了他们的第一台调整处理机的巨大原型机。他们决定使用点对点布线，以避免制作印刷电路板的费用和时间。原型机是在16IN/20IN的电路板上通过导线绕接技术而构建的。这一个原型机包含600多个门电路和2000个不同的信号网络。下面是有关信号网络的一些计数据：

网络的数目：2000
网络的平均长度：40IN（未端接的）
引线在接地平面上方的平均高度：0.2IN
线径（AWG30）：0.01IN直径
信号上升时间：2.0NS
转折频率：250MHZ（=0.5/2.0NS）

1、点对点布线的信号畸变

在NEWCO的设计中，上升时间为2.0NS，其电气长度为：

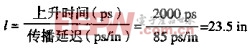
区分集总系统和分布系统的临界尺寸是：1/6=3.9IN

NEWCO认为，因为导线的平均长度基本上在这一界限之内，所以电路只会有很少的振铃。但是他们错了。

NEWCO认识到，当电路大于1/6时，将表现分布状态，他们知道，分布电路如果不端接，就会振铃。因为他们的电路是集总的，所以错误地认为不会振铃。

集总参数电路可能振铃，也可能不振铃，这取决于电路的Q值。电路的Q值显示出电路中信号衰减消逝的快慢。在低Q值电路中，信号衰减得很快，而在高Q值电路中，信号却来回振荡，经过几个振铃周期后才慢慢地消逝。Q值在技术上被定义为总存储能量与每个振荡周期所衰耗能量之比。从这个定义引出一个近似公式，将特定电路的最大过冲电压用Q值的一个函数来表示：

其中，V过冲=超出稳态输出电平的输出上升量，V
V阶跃=预期的稳态电平，V
Q=谐振参数（这里假设0.5）

图4.1中的理想二阶电路以时间常数2L/R衰减，完全符合上式。

根据经验，在一个理想阶跃的输入响应中，Q值为1的数字电路显示出16%的过冲，Q值为2的数字电路则显示出44%的过冲。任何Q值低于1/2的电路都不会过冲或振铃。一个电路上产生的振铃是电路本身的固有谐振频率和驱动器上升时间之间关系的一个函数。我们也将研究这个问题。

一旦我们知道了电路的电感，计算一个数字电路的Q值是很容易的。这提示我们关注点对点布线的基本问题：高电感。

当一个高电感引线工作于大电容负载的情况下时，会形成一个高Q值的电路。

我们可以采用附录C中列出的关于一个位于接地平面之上的圆柱体导线计算公式，来算出NEWCO系统中一个典型网络的电感L：

其中：L=回路电感，H
D=绕接线的直径，0.01IN
H=线路在接地平面上的高度，0.2IN
X=线的长度，4IN

采用式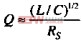（），可以计算出由驱动的源端电阻、导线的串联电感和接收器的负载电容组成的RLC电路的Q值：

R=30欧（一个TTL驱动器的输出电阻）
L=89NH（平均接线电感）
C=15PF（典型负载）

Q值为2.6意味着，对于一个理想的阶跃输入，将得到不小的振铃。由式（），预期最坏情况的过冲电压为：

V阶跃=3.7V（TTL阶跃输出）
Q=2.6（来自上式）

只有当NEWCO的逻辑驱动器在振铃频率以上传输有效能量时，这个最坏情况的过冲才会发生。采用下式可以找出振铃频率：

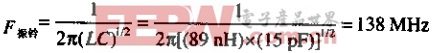
频谱宽度的衡量标准是转折频率，按照式（）的定义，NEWCO的逻辑门电路转折频率（250MHZ）远远高于振铃频率（138MHZ），因而存在大量的电能，可以引起振铃过程。转折频率如果正好等于138MHZ，振铃就将减小大约一半。转折频率更低的逻辑门电路产生的振铃还会更小。

如果完全在时域中考虑，我们可以断定，当上升时间等于振铃周期的一半时，最坏情况下的振铃被减少一半。上升时间越长，引起的振铃越小。相反，当上升时间远远小于振铃周期的一半时，将引起最坏情况下的振铃。

我们可以从Q值分析中发现更多的论据。我们知道，NEWCO的电路一般在138MHZ频率振铃，最大过冲为2.0V。根据线性电路理论可以知道，最坏的过冲总是发生在阶跃边沿后振铃周期的二分之一处，因此，能预知最大过冲将会发生在每个逻辑转换后的3.6NS处。