基于FPGA高精度浮点运算器的FFT设计与仿真
摘要 基于IEEE浮点表示格式及FFT算法,提出一种基2FFT的FPGA方法,完成了基于FPGA高精度浮点运算器的FFT的设计。利用VHDL语言描述了蝶形运算过程及地址产生单元,其仿真波形基本能正确的表示输出结果。
关键词 快速傅里叶变换;浮点;蝶形运算;VHDL
FFT作为数字信号处理中的重要的手段之一,主要在数字通信、语音信号处理、图像处理、功率谱估计、仿真、系统分析、雷达理论、光学、医学、地震以及数值分析等方面得到广泛应用。基于FPGA实现FFT,具有软件编程的灵活性及电路扩展性强等优点。随着集成电路技术进步和制造工艺水平的提高,FPGA芯片具有的功能越来越强,成为快速实时实现FFT的重要手段。采用基2法完成基于FPGA浮点运算器的FFT。
1 基于FPGA浮点运算器的FFT
1.1 浮点的IEEE标准格式
设计采用单精度浮点运算,IEEE定义的二进制浮点格式为32位。结构表示如图1所示。

将32位分为3部分:31位为符号位S,S为0时表示正数,为1时表示负数;30~23为指数E,是一个0~255之间的八位二进制数,其实际的指数是E-127,所表示的指数范围是2-127~2128;22~0表示尾数F,小数点前还隐藏了一位‘1’,单精度尾数可表示最大数为2(23+1)=16 777 216。因为10716 777 216108,所以单精度浮点数的有效位数是7位,即浮点数的精度为10-6。为方便FFT的运算,文中采用原码存储。
1.2 基2的DIT-FFT算法
在蝶形运算中采用复数形式表示数据。对于一个2点的蝶形运算,输入复数为A=x+jX,B=y+jY;经![]() 运算,输出复数A’=(x+ycosφ+ Ysinφ)+j(X+Ycosφ-ysinφ),B’=[x-(ycosφ+Ysinφ)]+j[X-(Ycosφ-ysinφ)]。
运算,输出复数A’=(x+ycosφ+ Ysinφ)+j(X+Ycosφ-ysinφ),B’=[x-(ycosφ+Ysinφ)]+j[X-(Ycosφ-ysinφ)]。
设计主要针对8点FFT进行设计,8点FFT算法的原理图如图2所示。
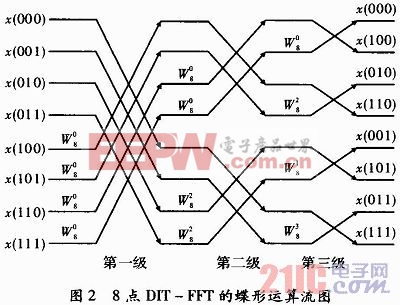
整个FFT过程中共有三级蝶形运算,每级蝶形运算有4个蝶形运算单元。在数据输入时按照自然顺序输入,最后倒序输出。
1.3 FFT处理器
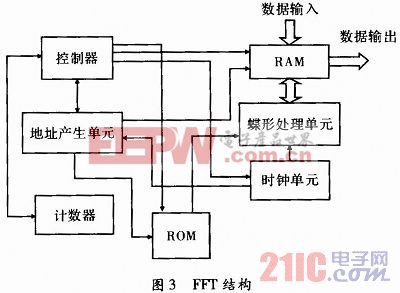
FFT处理器主要对数据进行蝶形运算及数据存取。设计采用基2蝶形运算器,包括存储器ROM和RAM,控制器及地址产生单元等。其FFT的结构模型如图3所示。
fpga相关文章:fpga是什么









评论