相位噪声和抖动的概念及其对系统性能的影响

时钟频率的不断提高使相位噪声和抖动在系统时序上占据日益重要的位置。本文介其概念及其对系统性能的影响，并在电路板级、芯片级和单元模块级分别提供了减小相位噪声和抖动的有效方法。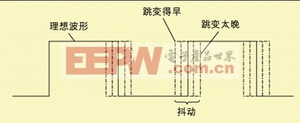

随着通信系统中的时钟速度迈入GHz级，相位噪声和抖动这两个在模拟设计中十分关键的因素，也开始在数字芯片和电路板的性能中占据日益重要的位置。在高速系统中，时钟或振荡器波形的时序误差会限制一个数字I/O接口的最大速率，不仅如此，它还会增大通信链路的误码率，甚至限制A/D转换器的动态范围。

在此趋势下，高速数字设备的设计师们也开始更多地关注时序因素。本文向数字设计师们介绍了相位噪声和抖动的基本概念，分析了它们对系统性能的影响，并给出了能够将相位抖动和噪声降至最低的常用电路技术。

什么是相位噪声和抖动？

相位噪声和抖动是对同一种现象的两种不同的定量方式。在理想情况下，一个频率固定的完美的脉冲信号(以1 MHz为例)的持续时间应该恰好是1微秒，每500ns有一个跳变沿。

但不幸的是，这种信号并不存在。如图1所示，信号周期的长度总会有一定变化，从而导致下一个沿的到来时间不确定。这种不确定就是相位噪声，或者说抖动。

抖动是一个时域概念

抖动是对信号时域变化的测量结果，它从本质上描述了信号周期距离其理想值偏离了多少。通常，10 MHz以下信号的周期变动并不归入抖动一类，而是归入偏移或者漂移。抖动有两种主要类型：确定性抖动和随机性抖动。确定性抖动是由可识别的干扰信号造成的，这种抖动通常幅度有限，具备特定的（而非随机的）产生原因，而且不能进行统计分析。造成确定性抖动的来源主要有4种：

1. 相邻信号走线之间的串扰：当一根导线的自感增大后，会将其相邻信号线周围的感应磁场转化为感应电流，而感应电流会使电压增大或减小，从而造成抖动。

2. 敏感信号通路上的EMI辐射：电源、AC电源线和RF信号源都属于EMI源。与串扰类似，当附近存在EMI辐射时，时序信号通路上感应到的噪声电流会调制时序信号的电压值。

3. 多层基底中电源层的噪声：这种噪声可能改变逻辑门的阈值电压，或者改变阈值电压的参考地电平，从而改变开关门电路所需的电压值。

4. 多个门电路同时转换为同一种逻辑状态：这种情况可能导致电源层和地层上感应到尖峰电流，从而可能使阈值电压发生变化。

随机抖动是指由较难预测的因素导致的时序变化。例如，能够影响半导体晶体材料迁移率的温度因素，就可能造成载子流的随机变化。另外，半导体加工工艺的变化，例如掺杂密度不均，也可能造成抖动。

随机抖动最基本的一个特性就是随机性，因此我们可以用高斯统计分布来描述其特性。例如，对一个只包含随机抖动因素的时钟振荡器的振荡周期进行100次连续测量，测量结果会呈高斯分布（或称正态分布）。在其均值加减1个标准差的范围内包含了所有周期测量数据的68.26%，在其均值+/- 2倍标准差的范围内包含所有测量数据的95.4 %，+/- 3倍标准差范围内包含99.73%的测量数据，+/- 4倍标准差范围内包含99.99366%的测量数据。

从这种正态分布中，我们可以得到两种常见的抖动定义：

1. 峰峰值抖动，即正态曲线上最小测量值到最大测量值之间的差距。在大多数电路中，该值会随测量样本数的增多而变大，理论上可达无穷大。因此，这种测量意义不大。

2. RMS(均方根)抖动，即正态分布一阶标准偏差的值。该值随样本数的增加变化不大，因而这种测量较有意义。但这种测量只在纯高斯分布中才有效，如果分布中存在任何确定性抖动，那么利用整个抖动直方图上的一阶方差来估计抖动出现的可能性就是错误的。

3. 多个随机抖动源可以用RMS方式相加。但要得到总的抖动，需要利用峰峰值，以便将随机抖动与确定性抖动相加。

相位噪声是频率域的概念

相位噪声是对信号时序变化的另一种测量方式，其结果在频率域内显示。图2用一个振荡器信号来解释相位噪声。

如果没有相位噪声，那么振荡器的整个功率都应集中在频率f=fo处。但相位噪声的出现将振荡器的一部分功率扩展到相邻的频率中去，产生了边带(sideband)。从图2中可以看出，在离中心频率一定合理距离的偏移频率处，边带功率滚降到1/fm，fm是该频率偏离中心频率的差值。

相位噪声通常定义为在某一给定偏移频率处的dBc/Hz值，其中，dBc是以dB为单位的该频率处功率与总功率的比值。一个振荡器在某一偏移频率处的相位噪声定义为在该频率处1Hz带宽内的信号功率与信号的总功率比值。

在图2中，相位噪声是用偏移频率fm处1Hz带宽内的矩形的面积与整个功率谱曲线下包含的面积之比表示的，约等于中心频率处曲线的高度与fm处曲线的高度之差。该曲线显示的是一个带噪声相角的振荡器的功率谱，这些噪声相角自身的波动见图3。

图2所示为振荡器的功率谱，而图3所示为噪声相角的谱，也叫相位波动的谱密度。对于距离中心频率足够远的偏移频率，从图2所示功率谱中测得的以dBc/Hz为单位的相位噪声等于图3中所示的该频率处相位波动谱密度的值。

图3中的密度谱是以对数坐标表示的，其中，相位噪声边带以1/fm2或20 dB/十倍频程的速度下降。实际上，在噪声边带中的某些地方，随着相关噪声过程的不同，相位噪声可能会以1/f3、 1/f2甚至 1/f0的速度下降。

下降速度为1/f2的区域被称作“白色频率”变化区，这个区域中的相位变化是由振荡器周期中白色的或非相关的波动引起的。振荡器在该区域中的行为由振荡器电路中元件的热噪声决定。当偏移频率足够低时，元件的闪烁噪声通常也会起作用，导致该区域的谱密度以1/f3的速度下降。

此外，还有一点值得注意，当图3中偏移频率趋于0时，边带噪声会趋于无穷大。这恰好与自由运行振荡器中理应出现的时序抖动行为相符。