保护走线实例详细分析
保护走线广泛地出现在模拟设计中。在一个两层板的音频电路中。没有完整的地平面,如果在一个敏感输入电路两边并行走一对接地的走线,串扰可以减少一个数量级。
本文引用地址:http://www.amcfsurvey.com/article/190130.htm在数字电路中,一个完整的地平面可以带来接地保护走线的大部分好处,但保护走线比完整的地平面更有优势。
依据经验法则,在两条微带之间插入两端接地的第三条线,两条微带之间的耦合则会减半。如果第三条线通过很多通孔连接到地平面,它们的耦合将再减半。如果有不止一个地平面层,那么要在每条保护走线的两端接地,而不要在中间接地。
在数字电路中,如果两条走线之间的距离足够允许引入一条保护走线,那么耦合通常已尼很低,而保护走线也没有必要了,详细情况参见下例。
例:保护走线的计算
在图5.12中,两条走线按三走线的宽度布放,这样刚好足够有一条保护走线的空间。估计串扰会是多少呢?

运用式 串扰的数值不可能更差于:
串扰的数值不可能更差于:
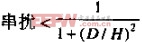
中心线间隔是0.040,而且走线高度是0.005,因此D/H的比值是8:
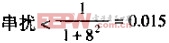
在一个数字系统中,这样的串扰是没有必要担心的。
多大串扰就太多了呢?在模拟系统中,大功率信号穿过低电平输入信号时需要非常高的抗串扰能力。那于混全使用不类型逻辑系列产品数字系统,当信号电压较高的元件与信号电压较低的元件接近的时候,将会对串扰问题比较敏感。
通常,对于同一种逻辑类型的数字系统,相近的线路之间的串扰电平在1~3%比较好。这里假设有一个完整的接地平面,从而使每条线只和它最近的线相互影响。来自其他较远的线的交叉耦合是可以忽略的。使用平行或指状接地系统时,许多线对互相影响,在计算一个给定信号总的串扰电平之前,必须算出所有串扰的影响之和。
图5.13举例说明了保护走线的典型应用。驱动器沿着走线A传输一个已知的电压阶跃,在走线B或走线C上可以接收到由这一信号引走的串扰。走线是26IN长,特性阻抗是50Ω。

图5.14显示了微带系统中各种不同的阶跃响应。
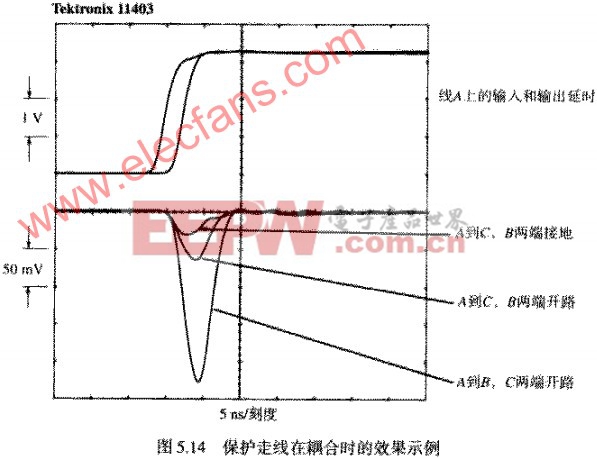
大的脉冲是线A和B之间的串扰,线C未连接。中间的脉冲是从A到C的串扰,线B未连接。如式
所预测的,它比A到B的干扰小4倍。
如果走线B的两端短接到地。则从A到C的耦合最小,这个耦合大约是中间走线耦合的一半。这就是保护走线的耦合减半的效果。










评论