电路板通孔的寄生电容分析

每个通孔都有对地寄生电容。因为通孔的实体结构小，其特性非常像集总线路元件。我们可以在一个数量以内估算一个通孔的寄生电容的值：

其中，D2=地平面上间隙孔的直径，IN
D1=环绕通孔的焊盘的直径，IN
T=印刷电路板的厚度，IN
∑=电路板的相对导磁率
C=通孔寄生容量，PF

当焊盘大小接近间隙孔直径的时候，焊盘会产生更多的电容。如果地层的间隙孔必须保持足够小，以维持地平面的连续性，那么就要减小或去除地层上的焊盘。对于走线通孔，如果在该层上有一些穿破，是不会有问题的。

通孔电容使数字信号的上升沿减慢或变差，这是它的主要影响。

上式假设每层上都有一个焊盘。有的设计者省略了一些布线层上没有边接走线的焊盘，这使得寄生电容略微减少。在许多实际情况下，寄生电容非常小，完全可以不考虑它。

如果必须要预先知道通孔的电容，可以使用一个实体模型来测算。当建立实体模型时，要使用电容的比例原理。

一个通孔或走线比例模型的电容是实际通孔电容的X倍，其中，X是模型的比例。

举例来说，图7.4表示了一个简单的焊盘模型，由铝箔和硬纸板构成，这是一个表面贴装设计走线通孔的100：1比例模型。中央的管子表示电镀孔的内表面。直径是1.6IN。管子两端的爆盘的直径是2.8IN。与地平面之间的间隙为5.0IN。从这些尺寸测算的电容值结果为11.0PF，按比例缩小100，在空气中的实际电容是0.11PF。由于实际的电容将会嵌入在FR-4中，其相对导磁率真为4.7，所以该通孔的电容将接近0.5PF。

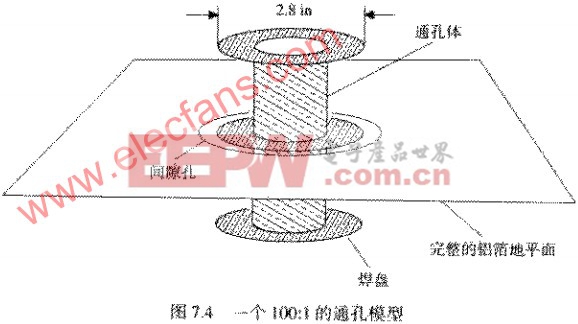
与实际完工的通孔电容相比，相对较大的11PF电容的精确测算要容易得多。此外，制作实体模型是非常有趣的事情。

让我们用上式再核算一下所测算的电容值：

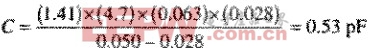
不要期望公式在所有的时候都会如此接近。

对于一个50欧传输线，这个通孔将会有多大影响呢？实际的通孔将使10~90%上升时间变差：

27PS确实是个非常小的时间间隔。

如果必须要经常进行焊盘的电容测算，可以投资购买电磁场模型软件。这些程序包能够精确地构造电感和电容三维空间模型。