基于FPGA的IIR数字滤波器的快捷设计

0 引言

IIR数字滤波器在很多领域中都有着广阔的应用。与FIR数字滤波器相比，IIR数字滤波器可以用较低的阶数获得较高的选择性，而且所用存储单元少，经济效率高。一个N阶IIR数字滤波器的系统函数为：

其线性常系数差分方程为：

用FPGA实现滤波的基本思想就是基于式(2)来实现的。如果知道了系统的输入序列(滤波器的输入)，那么，只要根据所给的滤波器的指标，然后通过MATLAB仿真出系数矢量b和a，再采用递推算法求解差分方程，就能求出输出序列(滤波器的输出)。

1 滤波器的MATLAB设计

由于本文采用巴特沃斯滤波器，故需要在工具箱中调用的两个函数buttord和butter的调用格式为：

其中N为滤波器阶数;wp和ws分别为通带截止频率矢量和阻带截止频率矢量，单位为π，一般需要模拟频率指标对采样频率的一半作归一化;Rp和As分别为通带最大衰减和阻带最小衰减，单位dB;wc为3 dB边缘频率矢量;b和a即为方程(2)中的系数矢量。

获得系数6和a之后，调用函数freqz(b，a，k，Fs)即可按照下式计算k点的复频率响应矢量H：

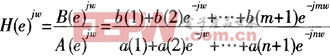
然后便可绘出K点的幅频和相频特性曲线，以用于检查计算出的系数是否满足所需要的滤波器指标。

2 编写VHDL语言代码注意事项

乘加运算过程中的数据是有符号的二进制补码，通常在Xilinx ISE集成开发环境下建立的VHDL源文件头部都会有“use IEEE.STD_LOG-IC_UNSIGNED_ALL;”，如将其改为“use IEEE.STD_LOGIC_SIGNED.ALL;”即应该包含有符号数运算程序包，这样就能保证代码中的所有std_log-ic_vector型数据按照有符号二进制补码的规则进行运算。

由于FPGA内部不能表示浮点数，因此只能用有限精度方法来实现数据的运算，即用数据(包括方程(2)的输入输出和系数)的整数部分(截去小数部分)作近似运算，且需要std_log-ic_vector数据类型来表示数据整数部分的二进制补码形式，但这样会产生截断误差。为了减小截断误差，应该将数据扩大适当的倍数(通常是2L倍，L为正整数)，以使小数部分可以忽略不计。扩大的倍数越大，截断误差就越小，得到的数据就越精确，但是，用来表示数据整数部分的std_logic_vector型数据长度会越大，这样就会占用越多的FPGA内部资源，因此，适当的选择数据扩大倍数是个关键。此外，各种数据转换为std_logic_vector型数据的长度选取至少应足以表示二进制补码(包括符号位)。若FPGA内部资源充足，可以通过增加std_logic_vector型数据长度来减小截断误差，提高运算精度。

通常由MATLAB仿真得到的系数b都远小于1，因此要适当选择正整数L。运算时可给系数b和a(a的第一个系数除外)同乘以2L，之后取整得到B=round(b*2L)和A=round(a*2L)

当前时刻输入的x(n)有时可能太小，为减小截断误差，应该选择适当的整数M，以给x(n)乘以2M，即给表示当前时刻输入的std_logic_vec-tor变量后补上M个‘0’。这样，得到的当前时刻输出y (n)就是扩大了2L+M倍的数据，应该除以2L+M才是当前时刻的真实输出。而VHDL语言不支持除法运算，故应采用截去末尾(L+M)位的方法来近似除法运算，这种做法相当于原始输出y除以2L+M之后截去小数部分。

在用示波器观测时，滤波器的输出波形可能带有许多大幅度尖锐毛刺，从而严重影响了滤波器的性能。毛刺是由于组合电路的竞争而使电路输出发生瞬时错误的现象，通常消除毛刺的方法是在具体的电路中加个锁存器。本文采取另一优化方法，即在源代码中通过符号“=”把输出信号赋给一个中间信号，再把中间信号作为输出，这相当于将信号作一个延时再输出。这种方法不需要知道具体的电路结构，也元需编写其它代码模块，因此优化更为简便快捷，而且优化效果非常好。

3 滤波器MATLAB设计的FPGA实现

下面以一个简单的低通滤波器设计实例来说明从MATLAB设计到FPGA实现的整个过程。该低通滤波器的系统采样频率为40 MHz，通带截止频率为1 MHz，阻带截止频率为5 MHz，通带内最大衰减为3 dB，阻带内最小衰减为40 dB，而对相位不作要求。