一种用于抗噪语音识别的动态参数补偿新方法
对于Log-Normal PMC(见图1-II),纯净语音模型同噪声模型的合并是在线性谱域进行。那么纯净语音和噪声模型的参数先要从倒谱域变换到对数谱域,然后再映射到线性谱域。在线性谱域进行模型的合并,然后进行相反的操作把模型参数映射变换回倒谱域。另一方面,Log―Add PMC(见图1一I)模型的补偿是在对数谱域进行。
通常的噪声信号有两类:卷积噪声(信道的频率响应)和加性噪声。在本文中仅考虑加性噪声情况。在文章中采用以下假设:1)噪声是平稳加性噪声,噪声和语音信号是相互统计独立的;2)每个子带的对数频谱域的特征(功率谱)分布被认为是(混合)高斯分布,Mel线性谱域的特征分布被认为是(混合)对数一正态分布。那么在Mel线性谱域第k个子带带噪语音特征Yk为:
![]()
其中Xk和Nk分别是线性频谱域的纯净语音和噪声子带特征(“观测”)。g是调节噪声和语音的缩放比例因子,为了表达简单起见,在后面的算法公式中省略此缩放比例因子g。那么对数频谱域子带的带噪语音特征Ykl同纯净语音特征Xkl和噪声特征Nkl的失配函数为:
![]()
2.1 静态特征补偿
对于Log-Normal PMC静态模型特征补偿的核心算法是对数谱域与线性谱域之间的非线性映射同线性谱域模型的合并,即:
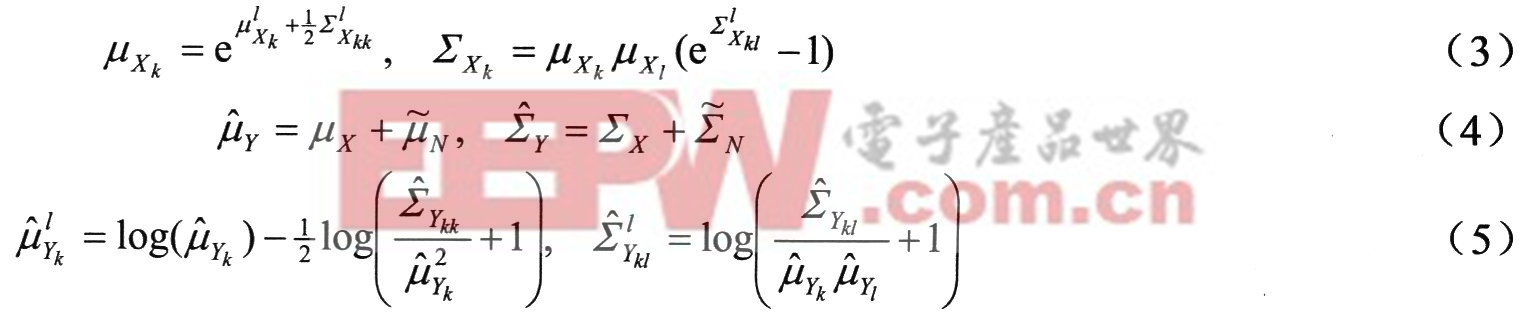
其中k、l分别为第k、l个子带。
对于Log―Add PMC静态模型特征补偿的只对均值进行补偿:
![]()
2.2 动态特征补偿
由于推导出严格的Log―Normal PMC动态特征补偿算法非常困难,目前对Log―Normal PMC的动态特征补偿一般采用粗略的补偿方法,只对其均值进行补偿。

对于Log-Add PMC其动态特征补偿算法为:
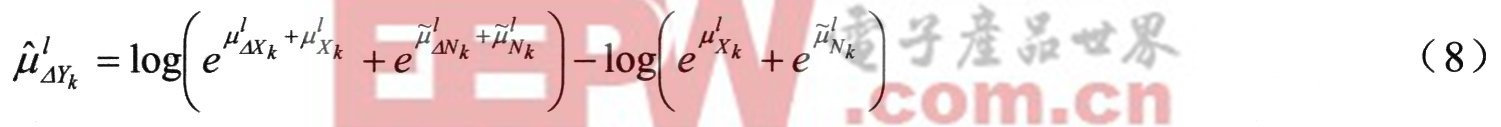
3 新的动态模型参数补偿方法
在本文中,使用静态“观测”的时间导数作为动态的“观测”。这样,动态特征的失配函数就应等于静态特征的失配函数的一阶导函数。根据(2),动态特征失配函数为:

定义一个附加的随机变量Zkl,定义为Zkl=Nkl一Xkl。由于Nkl和Xkl均为正态分布,并且他们之间相互独立,那么随机变量Zkl也是一个正态分布。其的均值和方差分别可以表示为μZkl=μNkl-μXkl和![]() 那么动态失配函数(9)就可以进一步改写成含Zkl的函数。
那么动态失配函数(9)就可以进一步改写成含Zkl的函数。

由于假设背景噪声为平稳加性噪声,那么噪声动态特征的均值就可以被近似为零。本文还假设附加的随机变量同语音和噪声的动态特征不相关。这个假设也是DPCM的核心本质假设。由于静态特征与其微分变换量之间是松相关的,所以这个假设是比较合理的。
3.1 均值补偿
依据失配函数(10)和上述假设,对数谱域的带噪语音特征的统计均值为:

其中

参数ti和ωi(i=l~n)是Hermite多项式Hn(t)的横坐标和对应的权值。










评论