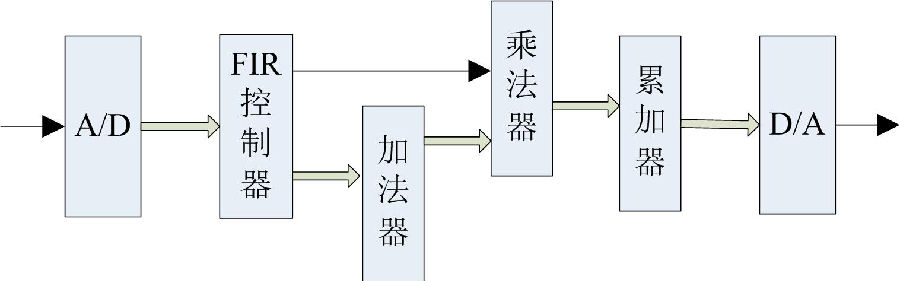
基于全相位幅频特性补偿的FIR滤波器设计
4.3 陷波器的设计
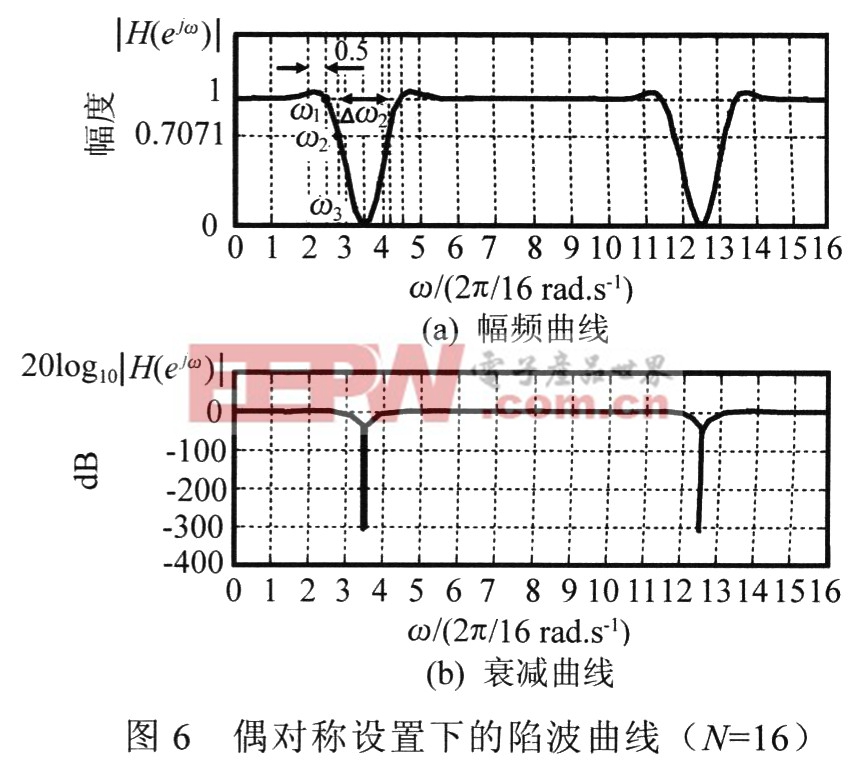
以具体实例来说明基于全相位幅频补偿法的陷波器的设计,以N=16为例,假设陷波偶对称频率向量H=[l 1 1 0 1 1 l l 1 1 l 1 0 1 1 1]T,其对应的幅频特性及其衰减特性如图6所示:由于幅频曲线严格通过(k+0.5)△ω的频率采样点,因此边界频率ω1=2.5△ω,ω3=3.5△ω,其中陷波点ω3处的衰减可达一300dB以下;3分贝角频率ω2=2.830△ω,3分贝带宽△ω2=1.34l△ω。
可将H衍生为两个频率向量Hl、H2:本文引用地址:http://www.amcfsurvey.com/article/188934.htm

令频移参数λ=0.25,将H1、H2、λ代入式(8)可得对应平移后的滤波器h1'、h2',将它们按式(12)叠加,即得复合后的陷波器系数:
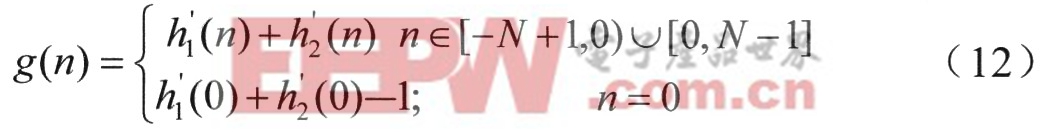
式(12)的g(0)要减去l,是因为h1'、h2'叠加过程中会引入大小为1的直流量,因而需要将此直流量减去。直流调整后的陷波曲线如图7所示,图7(a)表明:所有的边界频率点都精确地移动了0.25△ω,各边界频率变为但是图7(b)表明:陷波器的衰减性能变差,原因是陷波点移动后,ω1仍为子滤波器1幅值为0的频率设置点,但偏离了子滤波器2幅值为l的频率设置点。借助MATLAB可测出G'(ejω1)值,令μ=|G'(ejω1)|,用-μ值去替代H1、H2中幅值为0的频率采样值,重新代入式(9)和式(11)得到的衰减曲线如图8所示。


图8表明,经过μ值修正后的衰减特性仍可达-300dB以下。对应的陷波器系数如表l所示。
5 结论
本文提出基于全相位幅频特性补偿的FIR滤波器设计法,在偶对称的频率采样基础上,通过引入双相移组合和构造补偿滤波器的方法,它可把过渡带控制在频率采样间隔内。增大滤波器阶数N有利于控制过渡带内幅频曲线的线性度和减小边界频带宽度。并且在实际的数字滤波应用场合,可在不增大N的情况下,通过设置频移参数λ来解决对低通、高通、带通、陷波各滤波器的边界频率位置的任意点移动控制问题。






评论