基于全相位幅频特性补偿的FIR滤波器设计
控制边界频率一直是FIR滤波器设计的难题。传统的滤波器设计法,如频率采样法和窗函数法,因为无法控制临界频率,其应用受到限制。而一些现代滤波器设计方法,如神经网络法…、免疫算法等,这些方法设计的滤波器系数都是借助某种最优化算法对目标幅频函数进行逼近的过程中得到,但并没有解决在优化过程中如何控制边界频率问题。文献提出一种FRM(FreqLtency Responses Masking,频率响应屏蔽)设计法,它首先要设计两路满足幅度互补的原型滤波器,再将原型滤波器的每个延时器用M个延时器来代替(即内插过程),然后分别设计两路屏蔽滤波器去滤除由于内插而产生的镜像频率特性,最后将两路响应叠加即得最后滤波输出。这样产生的滤波器系数具有稀疏特性,而总的滤波器长度并不会明显增加,此方法因为可将过渡带限制在很窄的宽度内而得到广泛应用,但该方法存在原型滤波器与屏蔽滤波器的阶数、各频带波纹相互影响及性能匹配的问题,这些问题通常要用线性规化等复杂数学途径去解决。
本文在文献提出的全相位滤波器设计的基础上,通过变传统频率采样模式为偶对称的频率采样模式,并引入双相移组合和构造用于补偿的全相位单窗滤波器的方法,借助于MATLAB设计,使得FIR滤波器的临界频率的位置可通过改变参数λ得以解决,它具有无需多步迭代优化、设计方法简单的特点。
2 偶对称频率采样下的全相位FIR滤波器
2.1 全相位等效FIR滤波器的设计步骤
文献提出全相位DFT滤波器设计法,具有频率采样法和窗函数法的双重性质,并指出:滤波器性能可通过加前窗f或后窗b而得以改善,f和b的设定可分为三种情况:无窗、单窗和双窗。要设计N阶全相位滤波器,需先设置一频率向量H,最终全相位滤波器可等效为长度为2N-1的FIR滤波器,其设计可分为三个步骤:(1)对H进行IDFT生成h,再对h进行定义域延伸,形成(2N一1)长度的向量h’=[h(-N+1)…h(0)…h(N-1)]T。(2)将前窗f、后窗b进行卷积并归一化后生成卷积窗wc。(3)将h’、wc对应元素相乘即得等效FIR滤波器。根据以上步骤,将生成的2N-l长度的FIR滤波器g的系数推导如下:
设定频率向量为H=[H(O)H(1)…H(N一1)]T,假设满足传统对称H(k)=H(N-k),(k=1,…,N-1),令H对应的IDFT为k=[h(0)h(1)…h(N-1)]T。令WN=e-j2π/N,对h(n)的定义域进行延拓可得向量h’:

2.2 偶对称频率采样下的全相位FIR滤波器
事实上,H也可设为偶对称形式,即满足H(k)=H(N-1一k),(k=0,…,N-1)。如N=16时,可设为:H=[1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1]T,这时式(1)的IDFT结果为复数,从而式(4)的FIR系数也为复数。为得到实FIR系数,需要将式(4)的g乘以一相移向量v0=[v0(-N+1)…v0(一1)v0(0)v0(1)…v0(N-1)]T,其中![]() 结合式(4),其FIR滤波器系数变为:
结合式(4),其FIR滤波器系数变为:
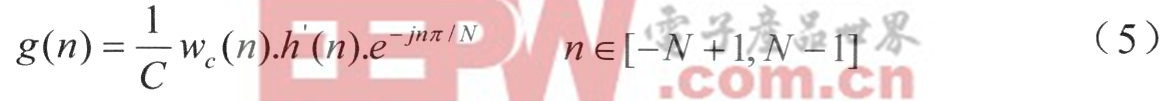
令频率采样间隔△ω=2π/N,文献证明:无窗和单窗全相位滤波器的传递曲线严格通过频率设置点k△ω,k=0,1,…,N―l而式(5)对滤波器系数乘以相移向量v0后,根据傅氏变换的频移性质,其频率设置点也相应右移0.5△ω,即严格通过ω=(k+0.5)△ω,这样就形成了偶对称的频率采样模式。例:当N=8时,令传统频采向量H=[1 1 l 0 0 01 1]T偶对称频采向量He=[1 1 0 0 0 0 1 1]T。则这两种模式在[O,2π)内的采样点分布如图1所示。

3 全相位幅频补偿法下的低通滤波器设计
以N=16为例,将偶对称频率采样向量H设为:H=[1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 l]T,在加汉明单窗的情况下,采用前面的全相位FIR滤波器设计步骤,可得到如图2所示的幅频曲线。






评论