基于小生境遗传算法的移动机器人路径优化
1.3 种群初始化
执行遗传算法的最优路径设计是必须对种群进行初始化,由于初始路径随机产生,各转向点坐标可能分布在整个规划区域范围内,包括可行的和不可行的,这样便增加了搜索范围。这里在可行区域内限制初始转向点,以加快遗传算法的收敛速度。具体做法为:判断该转向点是否在可行区域内,如果不是,则重新选取,直到坐标点符合条件为止。
根据规划环境的复杂度不同,最优路径中转向点的个数也是不确定的,一般来说,环境越复杂,转向点就越多,因此算法采用变长编码技术,通过对染色体进行删除、插入等操作,能够确定合适的转向点个数,使路径达到最优。但是,转向点数目太多,占用资源也就会太大,它将使运算速度变慢。因此,在运算过程中,设定最大转向点为Nmax,种群中每个个体的长度n满足2≤n≤Nmax。
采用小生境原理,将每一代个体划分为若干类,每个类中选出若干适应度较大的个体,作为一个类的优秀代表组成一个种群。
1.4适应度函数
所谓移动机器人的路径规划,指在起点和终点之间找出一条最短的可行路径,其约束条件是不与障碍物相交,同时移动机器人在行走中的转角不宜太大。该算法以两个条件作为规划路径的可行性评价函数,即路径总长度和各转向点拐角的平均大小,对于不可行的路径,对其适应度进行惩罚,使它的适应度差于可行路径。
(1)路径总长度。为了防止移动机器人与障碍物碰撞,应尽量使其与障碍物保持一定的安全距离。假设移动机器人的安全半径为r;移动机器人与障碍物的距离为d,则路径总长度Len由式(1)计算:
式中:d(pi-1,pi)为转向点pi-1与pi之间的长度。如果pi-1与pi之间的路径不可行,则使用惩罚函数法对其适应度进行惩罚。惩罚函数定义如下:

式中:ε为惩罚因子。路径的评价函数可以写为:
判断两点之间的路径是否可行,只需判断这两点的连线与障碍物的各边是否相交即可。根据几何学原理,判断两条线段是否相交可由以下两个步骤进行确定:快速排斥试验;跨立试验。鉴于文章篇幅,在此不再对这两个试验进行详细阐述。
评价路径是求路径长度最短的问题,通过惩罚因子,可以使不可行路径变长,从而降低它的适应值。
(2)路径平滑度。移动机器人的特点决定了它在行走过程中不宜以过大拐角进行转向,因此整条行走路径应趋于平缓而光滑,即每一转向点处的拐角值应尽可能小。这里假设拐角最大值不能超过π/2,平滑度可以使用路径的平均拐角值来计算:

式中:ξ为一个趋于零的常数(ξ>0);αi(0≤αi≤π,i=2,3,…,n-1)表示两向量AC,CB之间的夹角,B,C点的坐标分别为(xi-2,yi-1),(xi,yi),(xi-1,yi-1);k为αi中大于或等于π/2的个数,即当某一夹角大于或等于π/2时,对适应度进行惩罚。当n=2时,路径为起始点与终止点的连线。若其可行,则M值趋于0。可以看出,M值越小,路径的平滑度越好。
得到了以上两个条件的评价函数,就可以获得整条路径的适应度函数。采用各项评价函数加权求和是常用的确定适应度函数的方法。因为各个加权系数不是恒定不变的,而是随路径和障碍物的情况变化而变化的,所以这种情况下各个加权系数就很难调整和确定。因此,在确定适应度函数时,尽量使适应度函数的项数最少,但又必须把路径规划的两个条件融合在遗传优化过程中。这里采用评价函数相乘的形式,如式(6)所示。
f=1/(ML) (6)
以f作为选择操作的依据,则路径的长度和平均拐角越小,其适应度越好。
1.5 遗传算子
(1)选择算子。使用锦标赛选择法和精英保留法相结合的选择策略。采用在锦标赛选择法选择时,先随机在群体中选择K个个体进行比较,适应度最好的个体将被选择作为生成下一代的父体,参数K称为竞赛规模。这种选择方式能使种群中适应度好的个体具有较大的“生存”机会。同时,由于它只使用适应度的相对值作为选择的标准,而与适应度的数值大小不成直接比例,从而避免了超级个体的影响,在一定程度上避免了过早收敛和停滞现象的发生。精英保留法是当前种群中适应度最好的个体,它不参加遗传操作,可直接复制到下一代,替换经交叉和变异操作产生的子种群中适应度最差的个体,其优点是在搜索过程中可以使某一代最优个体不被遗传操作所破坏,这样可保证遗传算法以概率收敛到最优解。经验证明,保留占种群总体2%~5%数量的个体,效果最为理想。
(2)交叉算子。采用单点交叉法,在两个父体上分别随机选取一个交叉点(起点和终点除外),交换两个个体在各自交叉点之后的染色体。考虑到规划路径的长度是可变的,为了防止交叉操作后出现过于繁琐或简单的路径,对生成的新个体长度进行限制,即最大长度不能超过Nmax,并且不能产生回路,若不符合要求,重新获取两个父个体的交叉点。
(3)插入算子。设计了两种插入算子。第一种是有针对性的,即在连线穿过障碍物的两个转向点之间插入一个或多个转向点,使产生的路径避开障碍物,如图1(a)所示;第二种是一般意义上的插入,以一定概率插入一个随机产生的转向点,如图1(b)所示。
(4)扰动算子。同样设计了两种扰动算子,第一种只选取路径不可行的转向点来进行小范围的调整,使其路径可行,如图1(c)所示;第二种是不管路径是否可行,任意选取一个位置,以概率pm对其转向点坐标进行调整。在进化初期,不可行的解数量较多,调整的范围大一些。在进化后期调整范围逐渐缩小,如图1(d)所示。
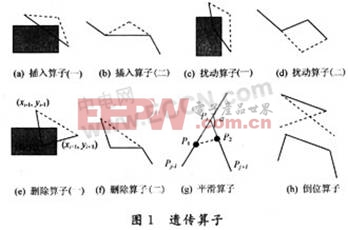
(5)删除算子。建立一个存储空间REC,在一条路径中,如果点(xi-1,yi-1)与点(xi,yi)的连线经过障碍物,但(xi-1,yi-1)与(xi+1,yi-1)的连线不经过障碍物,则将点(xi,yi)添加到REC中。如果REC不为空,则从中随机选取一点删除(见图1(e));否则,在路径中任意选取一个路径点,以概率pd进行删除,如图1(f)所示。





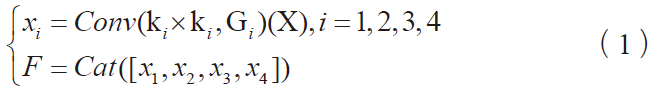

评论