基于遗传算法和扰动观察法的MPPT算法
3 遗传算法
3.1 优化变量选择及编码
通过前文分析,该系统的优化变量确定为Boost变换器的占空比D。因为D只能在0和1之间变化,所以采用搜索空间限定法处理约束条件。这里采用格雷码描述个体的基因。格雷码的优点是能使表现型相近的个体,其基因型(格雷码)也相近,从而克服自然二进制码所形成的“峭壁”。
假设格雷码为gngn-1…g2g1,那么格雷码的解码操作可以根据如下过程进行:
(1)格雷码gngn-1…g2g1转换为自然二进制码bnbn-1…b2b1:
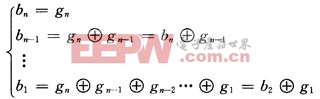
(2)自然二进制码bnbn-1…b2b1转换为表现型x:
3.2适应度函数的定义
在此采用式(3)所示的适应度函数,并定义Cmax=2 500。
3.3 选择操作
本文使用基于排序的适应度分配算法,种群按目标进行排序,个体的适应度仅取决于个体在种群中的位序,而不是实际的目标值。Blickle T的研究表明排序算法克服了按比例适应度计算的尺度问题,以及选择导致搜索带迅速变窄而产生的过早收敛,从而具有更好的鲁棒性。
这里将一个种群中的Nind个个体按适应度函数值从小到大排序,并取分布概率为:
Pi=2i/[Nind(Nind+1)], i∈[1,x]
根据已经计算出的个体概率,采用随机遍历抽样的的方法进行选择。该方法提供了零偏差和最小个体扩展,具有比轮盘赌算法更优越的性能。假设Nselect为需要选择的个体数目,按照等距离选择个体,选择指针的距离为1/Nselect,而第一个指针的位置由[0,1/Nselect]区间内的均匀随机数决定。
3.4交叉操作
交叉操作是遗传算法的重要步骤,它的目的在于产生新的基因组,同时也能有效地限制遗传信息的丢失。Syswerda等提出了均匀交叉算子,并把它和单双点交叉算子进行了函数优化实验对比,最后认为均匀交叉优于单双点交叉。
均匀交叉需要通过四步实现:
(1)根据交叉概率Pc随机生成交叉池;
(2)在交叉池中随机选择两个个体配对;
(3)随机产生一个与个体编码串等长的屏蔽字W=wd…wi…w2w1。其中d是编码串长度;
(4)若wi=1,则两个父代个体的第i位交叉,否则不交叉。
3.5变异操作
Deb等研究了交叉概率Pc和变异率Pm的相互作用对遗传算法的影响,结果表明交叉概率Pc对遗传算法性能的影响远比变异率Pm小。因此选用适当的变异率极其重要。在一般遗传算法中,种群使用的是固定的全局变异率,而且为了降低变异算子对模式的破坏作用,变异率一般都很小(小于0.1)。然而种群中的不同个体对整体进化的作用是不同的,优良个体之间的基因重组是群体进化的决定性力量,较差个体在种群中是一个不断被淘汰的过程。因此,应该对种群中的不同个体采用不同的变异率:一方面使种群中的优良个体具有较小的变异率,从而能够得到较好的保持,并通过交叉重组进行优良模式的累积;另一方面,种群中较差的个体能够通过较大的变异率增强种群的探索能力。
基于以上思想,在此采用如下变异率:
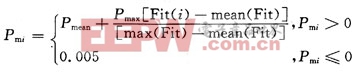
式中:Pmi表示第i个个体的变异率;Pmean表示具有群体的平均适应度的个体所具有的变异率;Pmax表示具有群体的最大适应度的个体所应增加的变异率;Fit(i)表示第i个个体的适应度。
3.6精英个体保留策略
为了提高全局寻优能力和收敛速度,本文采用保留精英个体的方法,即保留优化过程中每一代适应度值最高的个体,直接复制到下一代。
4 扰动观察法与遗传算法双模控制
4.1 扰动观察法
从图1可以看出光伏电池的输出功率具有式(4)所示的特性:

扰动观察法就是根据光伏电池的这一特性而提出来的。扰动观察法具有简单实用的优点,但是它在控制过程中,扰动步长ΔD的值对最大功率点控制的影响较大:当ΔD较大时,输出功率会在最大功率点附近具有较大的震荡现象;当△D较小时,系统对最大功率点跟踪较慢。
4.2 扰动观察法与遗传算法结合
遗传算法使用概率搜索技术,因此在恶劣环境中,它仍能准确搜索到最大功率点,但这也决定了它不可能使系统稳定工作于最大功率点。为了解决这个问题,本文引入扰动观察法与遗传算法双模控制。当最大功率点变化较小时,由小步长扰动观察法追踪最大功率点。








评论