二进制数及其他
原码 最高位表示符号,其他位表示数值,则这种表示方法就是原码。如
[+10]原=0000 1010B
[ -10]原=1000 1010B
反码 对于正数,反码和原码一样。对于负数,反码就是把原码符号不变,数值为取反,如
[+10]反=0000 1010B
[ -10]反=1111 0101B
补码
对于正数,补码和原码一样,对于负数,补码就是把反码加 1,如
[+10]补=0000 1010B
[ -10]补=1111 0110B
总结一下,对于正数,[X]补=[X]原
负数 ,[X]补=[X]反 +1
补码费劲的得到了有水木好处呢?我们用补码的话就可以直接带符号参与运算了。还是上面的例子。
[+10]补=0000 1010B
+ [ -10]补=1111 0110B
———————————————————
1 0000 0000B
得到的结果是 0,可能有人说了,不是最前面有个 1 的吗,怎么会是 0 呢。这里我们不要忘记了,在计算机 中,所有的数据位数是固定的,我们这里举例为 8bit 的例子,那么得到结果后我们也只能保存八位,你看看 上面的结果,一共有 8 个 0,计算机只能保存这 8 个 0,最前面的 1 是不算在结果里的。所以,得到的结果 就是正确的。
补码的运算中还有一个溢出的问题,大家可以试着用补码来计算一下 -98+(-50),你会发现得到 了一个最高位是 0 的八位数,也就是说,变成了一个正数。这就是超出了数据范围,产生了溢出。关于溢 出,因为不是重点,大家可以自己查书找到答案。
3 万物归于阴阳
《易传》记录“易有太极,始生两仪。两仪生四象,四象生八卦。这里所说的两仪,就是阴和阳。这 里所说的卦,是宇宙间的现象,是我们肉眼可以看见的现象,宇宙间共有八个基本的大现象,而宇宙间的万 有、万事、万物,皆依这八个现象而变化,这就是八卦法则的起源。而八卦的来源就是阴阳。 我国古代人们 发明的太极八卦用阴阳能够代表世间万物,那么由 0 和 1 组成的二进制数自然能够表示世间所有东西,而不 仅仅是几个数字。也就是说我们现实生活中的图形、图像、声音、文字、色彩等等,都可以用二进制数表 示,当然也可以在计算机中处理和显示出来。其实这个做到了的,否则我们今天也就不会有电脑里的图片、 音乐、视频、文字等等,我们今天的世界将不会这么多姿多彩。
那么,单纯的 0 和 1 如何表示世间的万物呢?这里要讲到一个词:代码。代码,从字面意思来看, 就是代替的码字,即我们找一组二进制数来代替,代替谁呢?代替世间的万物。到这里可能有人会有疑问 了?既然是代替的,必然不是真的,有什么用呢?自然有用,要是没用的话我们不会随时随地的使用。其实 我们就是生活在一个代码的世界里,如我们的名字就是一个代码,用汉字给我们每个人的一个代码,代表一 个个体。在学校里,每个学生都有一个学号,而这个学号就是一个代码,用一组十进制数来代表一个学生。 甚至我们所说的课桌,操场等等名词都是代码,用汉字来代表某个物体或者某种意义。代码到底有什么好处 呢?方便于我们的沟通和交流。还是以我们的名字为例来说。如果一个人叫“张三”,那么我们有事情要找 他,那么就喊“张三”,叫张三的人就答应了,于是你可以跟他交流了。合同上要双方签字,而就是签的名 字,合同签完后就可以存档了,不管经过多久,其他人看到这个签字,就知道这是经过双方本人认可了的, 而不需要双方两个大活人亲自告诉你说,这个合同我认可了的,因为名字就代表了其本人。如果我们不用代 码,那么一个合同文本上必须有两个人站在那里,证明合同双方都同意的,这是一件和荒唐的事情,文件柜 里站着两个大活人不是很滑稽和不可能的事情吗?所以,我们使用代码。注意的是代码就是代码,不是人本 身,你的名字不等于你这个人本身,它仅仅代表你这个人,我们不能说几个汉字和活生生的人是一样的吧。 每个人都有血有肉,有情感,但是汉字只是一些笔迹,不会有血肉。
代码,有任意性,就是我们可以用任何的东西来代表某个含义,如汉字里的“桌子”和英语里 的“desk“都是代表了同一种东西。这也表示这我们可以用随意的什么来代表我们每个人,我们的名字是汉 字,两个或者三个或者四个汉字,当然,我们也可以用数字来代表我们每个人,比如监狱里每个囚犯都有一 个编号,这个编号就是用十进制数来给每个人的代码。虽然代码有随意性,但是我们一般不会随意的进行编 写代码,而是按照某种规律来编码,因为有规律的代码使我们的维护更加方便。我们每个人的身份证就是一 个代码,是很有规律的,不知道有没有注意到这个规律。
代码就是用码字来代替,我们编写代码的过程叫做编码,有时候也称代码为编码。我们可以用 0 和 1
的二进制数按照某种规律排列起来代表任何一个事物,下面讲几种常用的代码。 二——十进制代码
二——十进制代码就是用二进制数对十进制数编写代码,也就是说用 0 和 1 来给十进制数的 10 个数
码 0~9 进行编码,也称为 BCD 码。接下来我们就看代码是如何进行编写的,需要多少位二进制数来进行编 码。表 3 列举了 1~4 位二进制数所能进行的编码个数,从中我们可以 知道,最少需要 4 位二进制数来进行编码。
表 3 1~4 位二进制数所能进行的编码个数
位数 | 1 位二进制数 | 2 位二进制数 | 3 位二进制数 | 4 位二进制数 |
代码 | 0 1 | 00 01 10 11 | 000 001 010 011 100 101 110 111 | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
代码数目 | 2 21 | 4 2 2 | 8 2 3 | 16 2 4 |
从表 3 中可以看到,有 N 位二进制数,那么代码的数量就是 2 N ,我们这里有 0~9 共计 10 个数,需要
多少位呢?3 位二进制数有 8 个代码,10 个数不够分,4 位二进制数有 16 个代码,还多了 6 个呢,我们怎 么办?我们可以想,如果有 10 个人来你家作客,如果你恰好有 10 张椅子还算好说,可是如果我们的椅子 不是恰好 10 把呢,你是提供 8 把椅子让 2 个客人站着还是提供 16 把椅子让椅子有空余呢?自然是提供 16 把椅子。多出来的 6 把椅子就让他空着吧。
我们在前面讲了,代码的编写具有随意性,也就是说你可以随意的编写你自己的代码,我们有 16 个 代码,给 10 个数进行编码,那么有多少种编码的方案呢?数学上问题就是从 16 个数里面取出 10 个数进行 全排列,计算的结果是大约有 10 亿种。这 10 亿种方案都是二——十进制代码,不过我们不可能用那么 多,代码的编写虽然有随意性,但我们进行编码不是自己一个人用的,还需要和别人交流,那么编写一个有 规律的和通用性的代码是必须的。理论上有无限种可能,但实际我们只使用其中的几种。那么我们常用的都 是哪种代码呢?最常用的就是 8421BCD 码了。这种编码的每位都有一个权值,恰好与自然二进制数的前
10 个数据相同,即用 0000(0)~1001(9)来表示十进制数的 0~9,从高位到低位的权值分别是
8,4,2,1,所以就称作 8421BCD 码。在 8421BCD 码中,每组二进制数各位按照加权系数展开便是它
所对应的十进制数。如 8421BCD 码的 0110 安权展开为
0110=0X8+1X4+1X2+0X1=6
所以 8421BCD 码 0110 表示十进制数 6。 这里一定要注意代码和我们前面讲的十进制数转换为二进制数相区别,对于同一个数,两种运算结果
是不一样的,例如十进制数 12,如果转换为对应的二进制数,那么结果是 1100 ,而如果转换为
8421BCD 码,那么结果为 0001 0010,也就是说,8421BCD 码就是严格的按照一位十进制数对应着 4 位二进制数来写,2 位十进制数,必然对应着 8 位二进制数,他们之间只有我们在进行 8421BCD 码编写的 时候给的对应关系,12 和 0001 0010 没有数值上的任何关系。
BCD 码还有 5421 码、余 3 码等等,大家可以看看数字电子技术的教材,我不一一的讲解了。
ASCII 码
ASCII 码(美国标准信息交换码),适用于所有的拉丁文字母,被国际标准化组织(ISO)批准为国 际标准,称为 ISO646 标准。我国相应的国家标准是 GB1988-80(即《信息处理交换用的七位编码字符 集》)。这里的 GB 读作“guo biao”(国标)而不是两个英文字母 ”G“ ”B“。ASCII 码 规定了信息交换用的
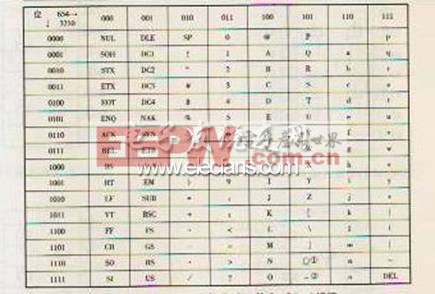
128 个字符。每个字符用 b7b6b5b4b3b2b1 七位来标识,通常最高位用 0 表示,使用 7 位二进制数来表 示所有的大写和小写字母,数字 0 到 9、标点符号, 以及在美式英语中使用的特殊控制字符。表 4 是 7 位
的 ASCII 码表。
表 4 7 位的 ASCII 码表
|
对于 ASCII 码,我们不要去记忆什么,只需要知道如何查看就好。
汉字编码
GB 2312 是一个简体中文字符集的中国国家标准,全称为《信息交换用汉字编码字符集基本集》, 又称为 GB0,由中国国家标准总局发布,1981 年 5 月 1 日实施。GB2312 编码通行于中国大陆;新加坡 等地也采用此编码。中国大陆几乎所有的中文系统和国际化的软件都支持 GB 2312。
GB 2312 标准共收录 6763 个汉字,其中一级汉字 3755 个,二级汉字 3008 个;同时,GB
2312 收录了包括拉丁字母、希腊字母、日文平假名及片假名字母、俄语西里尔字母在内的 682 个全角字
符。
GB 2312 的出现,基本满足了汉字的计算机处理需要,它所收录的汉字已经覆盖中国大陆
99.75%的使用频率。
对于人名、古汉语等方面出现的罕用字,GB 2312 不能处理,这导致了后来 GBK 及 GB 18030 汉 字字符集的出现。
GB 2312 中对所收汉字进行了“分区”处理,每区含有 94 个汉字/符号。这种表示方式也称为区位
码。
01-09 区为特殊符号。
16-55 区为一级汉字,按拼音排序。
56-87 区为二级汉字,按部首/笔画排序。
10-15 区及 88-94 区则未有编码。
举例来说,“啊”字是 GB2312 之中的第一个汉字,它的区位码就是 1601。 对于汉字编码,我们也不需要去管它,自然有计算机帮我们处理与之相关的问题,从信息处理的角度
来看,汉字处理也是非数值处理,和英文字母一样,需进行编码才能被计算机处理。 同样的,今天我们在计算机中所看到的每一样东西,包括图片、声音、视频等等都需要编码,也只有
进行了编码,我们才能在计算机中进行处理。我们的计算机不仅处理数值数据,还要处理大量的非数值数
据,而实际上,处理非数值数据要多的多。关于图片、声音、视频等的编码不是我今天的主题,请查阅相关
的专业书籍。
后记
上周有单片机课,讲到了二进制数,课堂上比较激动,下课后考虑到 09 级的学生在这个学期数电 、C 语言、单片机同时上课,对于二进制数可能会有理解上的难题,便决定把课堂上的讲课思路写下来,于是 就有了这篇文章。从上周四到现在,除开中间有其他的杂事,一共用了 2 天的时间写完。主要讲解了二进 制、十进制、十六进制的相互转换,带符号数的补码表示方法,编码的概念以及 8421BCD 码,ASCII 码, 简单的介绍了汉字的编码。对于八进制数,进制转换时小数的处理,因为我觉得这些不是最主要的,知道了十六进制数那么八进制数也就没什么困难了,至于小数的进制转换,原理和整数一样,在后续的学习中很少使用,所以不讲,上课的时候跟着老师听一遍就会的。补码运算,溢出没有过多的讲解,因为这部分理解上 有些困难,等这个学期结束了,再来看这两个问题比较好。我在写的时候就在不断的思考如何讲才能让学生逐步的,递进的理解,我是尽力的按照上课的时候讲 课思路来写的,语言也差不多是平时的用词,没有使用很正规的语法。有时候我发觉自己的思维有些跳跃,也不知道学生们能不能看懂这篇文章,如果有任何的问题,请告诉我。也欢迎你们把它分发到电子系其他班级同学那里,让大家得到方便。本文章不希望被转载,也不希望在没有得到我同意的情况下被任何刊物发表以及网站转载,但你可以 随意的下载阅读。除了大约 500 字是从百度上搜索得到以及图片扫描了其他教材的外,其他的文字都是我 逐字逐句的敲进去的,请尊重我的版权,下载后请保持原样,不要作任何修改,版权属于作者本人。



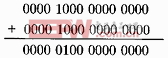

评论