二进制数及其他
(超过 255 的数据建议大家用计算器来求解,手算或者心算就太费劲了。)。这个方法就是利用权,一个 4
位的二进制数,它的每一位的权恰好是 8421,如图 3。
128 64 32 16 8 4 2 1
图 3 二进制数每一位的权
接下来我们就以一个具体的例子来说明这种方法的使用。先看二进制数转换为十进制数的例子,就是 上面说的 10110 吧,把它的每一位的权都标出来,如图 4。
16 8 4 2 1
1 0 1 1 0
图 4 二进制数转换为十进制数的例子
我们只要把数值是 1 的位的权加起来就可以得到对应的十进制数,即 16+4+2=22,完全一样。但是比列
式子快速的多了,如果熟悉了每一位的权之后我们都可以心算,快速的算出结果为 22。
接下来讲十进制数转换为二进制数的例子,把十进制数 55 转换为二进制数。开始运算之前先把图 3
画在草稿纸上,然后开始填 1,首先,55 在 64 和 32 之间,所以 64 处不能是 1,我们在 32 处写 1,这个
1 的权是 32,那么我们还剩下 55-32=23,比 16 大,我们在 16 的位置上写 1,这时候我们还剩下 23-
16=7,接着我们就可以在 4、2 和 1 的位置上分别写一个 1,32+16+4+2+1 恰好等于 55,所以我们在 其他的位置上写 0,把这个数写出来 110111,就得到了转换后的二进制数了。整个过程如图 5 所示。
|
采用这种方法可以快速的实现二进制数和十进制数的相互转换,这里要提醒大家一点了,我们只需要练习十
进制数 255 以内的数据和二进制数之间的相互转换就可以了,太大的数据交给计算器来运算就好了,千万 不要为难自己,非要去计算 52369 的二进制数,那将让你失去许多乐趣的。相对于二进制数来说,我们只 要能计算 8 位以内的二进制数转换为十进制数就可,超过 8 位的还是交给计算器吧。当然了,每个人都有自 己的自由,如果某人要手工计算 32 位二进制数转换为十进制数或者把一个上亿的十进制数转换为二进制 数,我也没有办法。
在现实生活中,对于十进制数,我们自动的根据数据的大小调整数位,15 有两位有效数字,那么我
们写 15 就好,那么没有人会写成 00015 的,同样的 369 有三位有效数字,也没人会写成 00369,因为 在数字的前面加 0 不改变大小,所以我们通常是省略前面的 0。但在数字电路中有另外一种情况,譬如我们 制造好了一个电路后,能表示 8 位二进制数,那么就必须制造 8 个基本元件,每个基本元件存储一个二进制 数,那么表示任何一个数,都是这 8 个基本元件作为一个整体来表示的,这样就会遇到多余的 0,如表示十 进制数 30,那么就是 00011110,前面的 0 你不能省略,因为你不能说最前面的 3 个元件不存储数据了, 再者,电路造好之后你也不能随便的用刀砍掉一部分。所以,在我们数字电路以及单片机课程中,一般遇到 的二进制都是位数固定的,我们在写这些数据的时候一定不要省略前面的 0,那么这个固定的位数是多少呢?
8 的倍数,也就是说,一般来说都是 8 位数一组,或者是 16 位,32 位,64 位,128 位等。
针对单片机中二进制位数固定这一特点,这里有几个名词:位(bit),字节(Byte),字
(Word)。其中位就是二进制位,1 位就是一个二进制位,称为 1bit,简写 1b,1 字节代表 8 个二进制的
位,1Byte=8bit ,1 字代表 2 个字节,1Word=2Byte。Byte 可以简写作 B,我们可以得到如下公式:
1B=8b,1Word=2B=16b
随着计算机技术的发展,数据越来越多,我们还有几个单位,KB,MB,GB,TB,其关系为:
1KB=1024B= 210 B
1MB=1024KB= 220 B
1GB=1024MB= 230 B
1TB=1024GB=2 40 B
2.3 十六进制数出世
数字电路中都用二进制数,计算机中当然也用二进制数,而我们要与这些电路打交道,必然要会二进 制数,大家看看以下这几个二进制数,然后抄一遍:
第一个数:00001101
第二个数:0101001110011010 的三个数:11100101011100110011001011101111 第四个数:
1101010001111000001110110110111011100110000011100100010010011100
第一个数是 8 位,写下来没什么太大的关系,第二个数是 16 位,仔细的看一下,抄写也可以,第三个是32位,我想可能要非常吃力的才能写下来,也许还要多次才能正确的抄写下来,那么最后一个 64 位的,有人有勇气面对它吗?如果是写满了 0 和 1 的 20 张 A4 的纸呢,任是谁也会崩溃的,太苦恼了,如果每天都是 看到的都是这些数字,也只有神仙才可以做得到了。这还不算,怕的就是出错了,满目都是 0 和 1,稍微错 了一位,面目全非了,所有的工作就要重新来过。有人会说,我直接转换成 10 进制数来读写好了。但是二 进制数转换为十进制数太繁琐,谁能告诉我最后一个数对应的十进制数是多少呢?
二进制数难读,难写,数据位数多,写和读都不方便,而我们却不能不看,不能不用,因为我们不能
不用数字电路,也不能不用计算机。当问题出现了,我们就要解决它,于是出现了十六进制。 十六进制有十六个数码:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,基数是 16,
运算时逢十六进一。为什么说十六进制数解决了二进制数读写困难,也没有十进制数转换繁琐的困局呢?因 为十六进制和二进制数相互转换非常简单,4 位二进制数对应于一位十六进制数,这样就可以把上述冗长的 二进制数转换为十六进制数。上面四个二进制数转换为十六进制数为:
第一个数:0D 第二个数:539A 的三个数:E57332EF
第四个数:D4783B6EE60E449C
当你看到上面这组数据的时候,读和写的时候要轻松的多了吧,这样我们被前面二进制数打击的信心 又回来了。那么你一定迫切的想知道二进制数和十六进制数是如何转换的吧。好吧,我们就来讲二进制数和 十六进制数的转换。
二进制数转换为十六进制数:4 位一组,分别转换;
十六进制数转换为二进制数:1 位转换为 4 位,原序排列。 在进行学习二进制数和十六进制数转换之前,先看一个表格,
表 2 十进制数、二进制数、十六进制数的对应关系
十进制数 | 二进制数 | 十六进制数 | 十进制数 | 二进制数 | 十六进制数 |
0 | 0000 | 0 | 8 | 1000 | 8 |
1 | 0001 | 1 | 9 | 1001 | 9 |
2 | 0010 | 2 | 10 | 1010 | A |
3 | 0011 | 3 | 11 | 1011 | B |
4 | 0100 | 4 | 12 | 1100 | C |
5 | 0101 | 5 | 13 | 1101 | D |
6 | 0110 | 6 | 14 | 1110 | E |
7 | 0111 | 7 | 15 | 1111 | F |
我们只要对照这个表格,就可以很轻松的进行二进制数和十六进制数的转换了。下面用具体的例子来说明。
例 1 把二进制数 1011 0110 转换为十六进制数
首先把二进制数分组
1011 0110
B 6
则二进制数 10110110 转换为十六进制数就是 B6 了。更多的位数一样的转换。
例 2 把二进制数 1110 1100 0111 0010 转换为十六进制数 把二进制数分组
1110 1100 0111 0010
E C 7 2
转换的结果为十六进制数 EC72
反过来,十六进制数转换为二进制数则反过来,直接一位变为 4 位就可以了。例如把十六进制数
A157 转换为二进制数,则
A 1 5 7
1010 0001 0101 0111
转换后的结果就是 1010 0001 0101 0111。
正因为十六进制数和二进制数的相互转换不需要进行计算,只是简单的替换就可以,所以我们在很多 场合下经常用十六进制数来代替二进制数,在学习单片机课程的时候,经常遇到十六进制数,所以必须掌握 十六进制数和二进制数的相互转换,而且要能熟练的转换。针对表 2,我建议大家就用 8421 法来记忆,数 字都很小,即使记不住,临时来计算也很快的。
二进制数和十六进制数能够相互转换,那么十进制数和十六进制数的相互转换怎么做呢?十进制数和 十六进制数可以直接相互转换,也可以用加权法,十六进制数的每一位的权是 1,16,256,4096……数 据运算量比较大,所以我们就简单的计算一下 2 位的十六进制数和十进制数的相互转换,太大的数据就不要 为难自己了,用计算器吧。我的方法是先转换为二进制数,然后再把二进制数转换为十进制数,这样手算的 速度要快些。反过来,要把十进制数转换为十六进制数,也是先把十进制数转换为二进制数,然后在转换为 十六进制数。
我们现实生活中使用十进制数,而计算机中使用二进制数,为了读写的方便,我们发明了十六进制 数,并且通过上面的学习我们也知道了如何快速的在这三种进制数据之间相互转换,应该没有上面太大的问 题了。但是还有一个问题,大家再看一看表 2,二进制、十进制、十六进制数据他们的数码,你会发现数码 有重合的部分,这就有问题了,如果出现了一个数据,如何知道是那种进制的数据呢?如
1110,145,562。可能有人会说,第一个数是二进制数,第二个和第三个数据是十进制数。但这是错误 的。就如一件衣服 200 元,如果在重庆,那么就是 200 人民币,如果是在香港买的,那么就是 200 港元, 如果你跑到英国去买,那么可能会是 200 英镑或者 200 欧元了,这可是不一样的,而且差别很大。这个时 候你再来看看 1110 和 145 这两个数,到底是什么进制的数据呢?不知道,除非做了说明。这就是我要讲 的另外一个问题,对于任何一个数字,我们必须作出说明是什么进制数据才有意义,否则我们不知道它的真
实大小。那么如何来区分这三种进制的数据呢?我们采用在数字的末尾加一个字母来表示。
二进制的英文单词是 Binary,十进制的英文单词是 Decimal,十六进制的英文单词是
Hexadecimal,所以我们就在二进制数后面加字母 B ,在十进制数后面加字母 D ,在十六进制数后面加字
母 H,这样就可以区分这三种进制的数据了。如 1010B,145D,562H 等等。因为我们现实生活中用的最 多的是十进制数,所以十进制数后的字母 D 可以省略,直接写 145,就如我们在中国买东西,标价是 200 的话默认单位就是人民币了,但二进制数和十六进制数后的字母不能省略。
2.4 负号的解决之道
以上在讨论数值的时候都只考虑了正数的情况,其实我们还使用负数以及小数,鉴于小数在我们课程 的学习阶段用的不是很多,特别是 9051 单片机,对于小数的运算非常不擅长,所以也就很少用到了,自然 不会讲太多。接下来我们就仅讨论负数的问题。
在数学运算中,表示一个数的正负,我们在数据的前面加上一个 正号或者负号(+/-),但是在计算 机中,对于这个正负号的表示就有点问题了,计算机中只能使用 0 和 1,没法使用+ -,那么我们如何表示 一个数值的正负呢?方法是用 0 和 1 来表示正负号。正常的情况下,我们用 0 来表示正号,1 来表示负号。 这样,我们对于一个数值就有两部分构成,符号位和数值位,符号位用 0 和 1 来表示正负,数值位表示大 小。计算机中的数值有很多,为了防止符号位和数值位不对应,我们一般把符号位和数值位作为一个整体来 处理。前面我们讲过,在计算机中经常用到的单位是 Byte,有 8bit,我们就把最高位作为符号位,其他的 7 位作为数值位。如图 6。
D7 D6 D5 D4 D3 D2 D1 D0
符号位 数值位
0 正数
1 负数
图 6 符号位和数值位
这样我们就可以用二进制数来表示负数了。如
+10=0000 1010B
-10=1000 1010B
这样我们就不怕负数了。我们来计算一下+10 + (-10)的结果。在计算机中,+10 和-10 我们已经转化 为二进制数了,这里直接列竖式相加就可以了
0000 1010
+ 1000 1010
————————————
1001 0100
为什么结果不是 0?难道+10 +(-10)不等于 0?答案肯定是 0 的,绝对是二进制数运算出错,可是错误
在哪里呢?大家思考一下数学中对于两个数据相加是如何做的?首先是比较两个数的符号,如果符号相同, 那么两个数值相加,符号不变,而如果两个数值符号不同,则比较一下哪个数值大,用数值较大的减去数值 较小的,符号用数值较大的符号。也就是说,我们数学上计算的时候是分情况的,而在上面的式子中,我们 把符号也参与运算了,并没有比较两个数的数值大小。




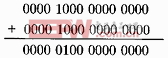

评论