实现电流零纹波的耦合电感计算
摘要:研究了两电感互相耦合以后实现其中某一个电感上电流纹波为零的现象。论述了实现零纹波的条件,从等效电路观点解释了其原理。着重分析了耦合磁路的等效磁阻模型,并由此模型给出了实用的耦合磁路参数计算公式。
本文引用地址:http://www.amcfsurvey.com/article/179419.htm关键词:耦合;纹波;磁阻;磁阻模型
1 引言
开关电源效率高,体积小,稳压范围宽,应用日益广泛。但它有一个固有的缺点:输出纹波(开关噪声)大。这使得开关电源无法用于音响等要求低噪声电源的设备。
在开关变换器中,如果两电感两端的电压波形一致,那么这两个电感就可以耦合到一个磁芯上,从而明显地减少磁性材料的体积和重量。Cuk变换器的输入输出电感就符合这样的条件,通过合理地设计两电感的耦合结构,使输入输出两个换能电感适当耦合,可使某一电感电流低纹波甚至零纹波。近年来,电源工作者深入研究Cuk变换器这一特性并努力使其实用化。
2.1 以L1和L2互相耦合为例来说明零纹波实现条件[1]
如图1所示,由文献[1]的论述可知,当两电感L1(N1匝)和L2(N2匝)耦合时,Lm为激磁电感,Li1为原边漏感,Li1为副边漏感,折算关系为L1=Lm+Li1,L2=Lm+Li1,显然电感两端的纹波电压为
 (1)
(1)
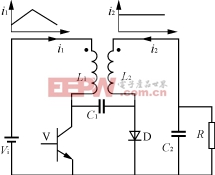
图1 电感耦合Cuk变换器
令Ve1=Ve2=Ve,联解式(1)可得
![]() (2)
(2)
式中:Lep=L1+![]() Lm(3)
Lm(3)
称为等效原边电感
Les=L2+![]() Lm(4)
Lm(4)
称为等效副边电感
设耦合系数k=![]() (5)
(5)
电感匝比n=![]() (6)
(6)
则式(3)、(4)变为
Lep=L1![]() (7)
(7)
Les=L2![]() (8)
(8)
由式(7)、(8)可得出如下结果:
当n=1时,
LeP=L1(1+k),LeS=L2(1+k)
其效果是使电感增加(1+k)倍,使原副边纹波电流减小到1/(1+k)。
当n1,即N1N2,并且k=n时,
LeP=L1,LeS→∞
其效果是使原边纹波不变,副边纹波电流为零。
当n>1,即N1>N2,且k=1/n时,
基尔霍夫电流相关文章:基尔霍夫电流定律
dc相关文章:dc是什么
电流传感器相关文章:电流传感器原理









评论