基于SI滤波器的一种小波变换的实现
摘要:文中在应用对数域电路的基础上,提出了一种新型的连续小波变换方法,它通过对母小波的一种数值逼近得到小波函数的有理公式,并以Marr小波为例来模拟这个逼近过程,并用Matlab对逼近过程进行仿真。仿真结果显示,该研究成果为实时小波信号处理提供了新的途径,拓宽了集成电路的应用范围。
关键字:对数域积分器;小波变换;滤波器;低电压;低功耗
目前模拟集成电路设计的主要研究方向是低电压、低功耗电路的实现。对数域电路的设计采用了瞬时缩展技术,很好地解决了在低电源电压下保持动态范围和高频率工作点的问题。小波变换是80年代后期发展起来的应用数学分支,是Fourier变换发展史上里程碑式的进展,以Fourier变换理论为基础,但在许多性质上又要优于Fourier变换。小波变换作为时一频分析方法,能聚焦到信号时段和频段的任意细节,具有“自适应性”和“数学显微镜”的美誉而得到越来越多的重视,成为信号处理、图像压缩和模式识别等众多领域中一个非常有效的数学分析工具。
开关电流(简称SI)电路是应用电流取样表示信号的模拟取样数据电路,属于电流模电路,具有一般电路不具有的优点,与标准数字CMOS工艺兼容。开关电流集成电路电路作为新型的模拟电路,运行在电流模式状态下,具有低电压、低功耗的特点。
基于以上现状,用开关电流技术实现连续小波变换是一个非常好的选择。本文采用对数域积分器代替滤波器中的积分单元,其研究成果为实时小波信号处理提供了新的途径,同时也拓宽了集成电路的应用范围。
1 小波变换实现过程
连续小波变换的实现可以简要概括为:仿真母小波φ(t)并使用它来实现滤波器电路。该方法的实现取决于小波函数类型。本文以Marr小波为例,它可由麦可劳林公式逼近得到,但是同样可以获得可选择的传递函数。
1.1 小波变换
设信号x(t)是平方可积函数,φ(t)是被称为基本小波或母小波的函数,则:
![]()
(1)式称为x(t)的小波变换,其中a>O是尺度因子,b反映位移,其值可正可负。从定义上看,小波变换相当于信号x(t)与![]()
的卷积。一个滤波器电路的输出是滤波器脉冲响应与输入信号卷积,因此,实现对信号的CWT可以使信号通过滤波器来实现。
1.2 小波函数的逼近实现
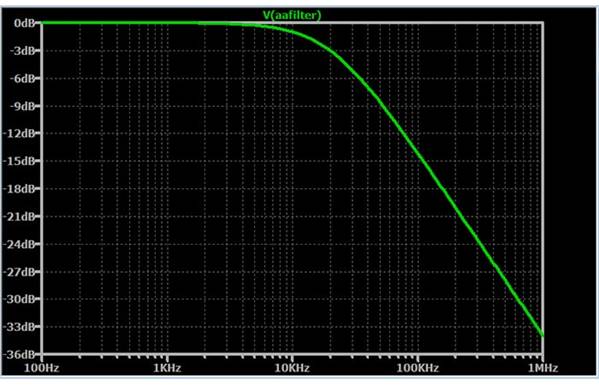
这里以Marr小波(见图1)为例来研究小波函数的实现方法,它的时域表达如下式所示:
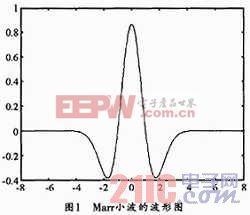
![]()














评论