基于C++的电力潮流计算牛-拉法与P-Q法的分析比较

1. 引言

潮流计算是研究电力系统稳态问题的基础，在应用计算机计算电力系统潮流分布以来，先后出现过以节点导纳矩阵为基础的逐次迭代法，即导纳法，和以阻抗矩阵为基础的逐次代入法，即阻抗法。针对阻抗法占用计算机内存大的问题，又出现了分块阻抗法及牛顿-拉夫逊法(Newton-Raphson)，而NR法也解决了导纳法收敛性差的问题。PQ分解法是使用极坐标表示时的NR法，既可用于离线潮流计算，更能够应用于在线潮流计算。

本文针对NR法和PQ法，在Windows环境下，使用C++语言开发出了相应的计算工具，对同一个算例分别使用不同工具，将得到的两种结果进行比较，发现对不同复杂度(本文以节点数目多少来定义网络复杂度高低)的算例，应当选择合适的算法程序以使收敛性和计算速度能同时满足要求。

2. 潮流计算的基本原理

潮流计算时对每个节点给出两个运行参数作为已知条件，另外两个作为待求量。由原始数据的给出方式，节点一般分3类：

(1)PQ节点：已知节点有功功率及无功功率(P,Q)，待求量为电压幅值和电压相量角度(V, )。

(2)PV节点：已知节点有功功率及电压幅值(P,V)，待求量为无功功率及电压相量角度(Q, )。

(3)平衡节点：此类节点一般在系统中只设一个。给定该节点电压的幅值V及电压向量角度 = ，待求量为该点有功功率P及无功功率Q。本论文中所用算例均只有一个平衡节点。

2.1 NR法的基本原理

牛顿-拉夫逊法通过逐次线性化把非线性方程式的求解过程变成对相应的线性方程式的求解过程。其修正方程式为：

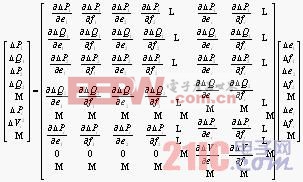
(1)

2.2 PQ法的基本原理

PQ分解法是在对采用极坐标表示的NR法进行有效简化的基础上发展而来，NR法的核心是求解修正方程式。高压电力系统中有功功率潮流主要与各节点电压向量角度有关，无功功率潮流则主要受各节点电压幅值的影响。忽略可以不计入在内的因素，其修正方程式采用极坐标表达为：

(2)、(3)与功率误差方程式

(4)和

(5)

共同构成PQ分解法迭代过程中的计算公式。

3. NR算法和PQ算法的C++编程方案设计

考虑到计算工具的通用性和可扩展性，设计时应将各部分功能进行模块化处理，以利于缩短开发周期，并实现不同算法中功能相同模块的重复使用，提高程序代码使用率。因而选择VC++6.0中STL所提供的常用容器类模板Vector，Complex和String编写程序代码：Vector模板类用于对向量类型数组进行操作，且Vector对象运行时可以动态改变自身大小以便容纳任何数目的元素;Complex模板类用于复数存储和操作;String模板类用于字符串操作。正是基于C++通用库STL模板类功能便于实现模块化，而无论采用哪种算法都须对电压，电流及功率复数向量进行处理。此外，还要适应不同规模的算例，因此利用STL通用库模板类进行编程成为本论文的首选。其次，网络参数的输入统一采用电气和电子工程师协会推荐使用的标准数据格式：IEEE通用数据文件格式(Common Data Format),CDF作为电网的拓扑结构输入文件，另外每个算法程序还要给出各自运行耗时，方便计算结果对比。

3.1 文件输入输出模块

文件输入模块完成对电力系统网络的拓扑结构以及各个节点和各条支路的参数信息的读取和存储，供计算使用。首先建立一组输入文件，以5节点网络为例，按照CDF格式建立输入文件，包含各节点参数和各支路参数，以“005IEEE.dat”作为文件名存档。编程时定义节点信息结构体(BusData)和支路信息结构体(BranchData)。母线节点信息(BUS DATA FOLLOWS)包含：节点编号number、节点名称name、负荷区编号LoadFlowAreaNumber、损耗区编号LossZoneNumber、节点类型Type、迭代后的电压值FinalVoltage、迭代后的电压向量角度(此处为弧度制)FinalAngle、负荷有功LoadMW、负荷无功LoadMVAR、发电机有功GenerationMW、发电机无功GenerationMVAR、基准电压BaseKV。支路信息(BRANCH DATA FOLLOWS)包含：支路起始节点TapBusNumber、支路终端节点ZBusnumber、负荷区LoadFlowArea、损耗区LossZone、支路类型Type、支路电阻值BranchR、支路电抗值BranchX、支路对地导纳值LineChargingB、变压器变比TransformerFinalTurnsRatio。通过ifstream DataFile(filename.c_str())语句打开数据输入文件，对输入文件数据流操作，将相应信息导入与之对应的结构体变量，完成输入文件模块化。

文件输出模块用来输出并保存潮流计算结果，利用outputfile语句对NR算法和PQ算法每次迭代时各个变量的初值和计算后的终值输出，并将最终结果存入“xxxieee_NR_Result.dat”和“xxxieee_PQ_Result.dat”文档。

3.2 NR算法模块化函数编程及流程图

(1)导纳矩阵生成模块：根据网络拓扑结构计算出导纳矩阵;

(2)节点功率误差模块：根据功率误差公式计算出各节点功率误差;

(3)雅可比矩阵生成模块：由NR法修正方程式系数矩阵公式计算出雅可比矩阵;

(4)修正方程式求解模块：解修正方程式得到修正量;

(5)节点电压修正模块：用修正量去修正各节点电压值。

流程图见图1。

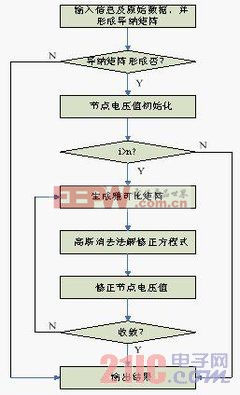
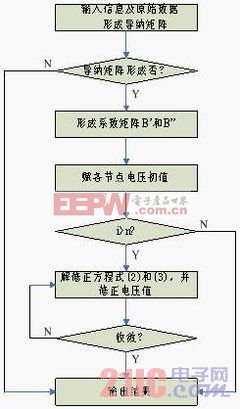
图1 NR算法模块化函数编程及流程图 图2 PQ算法模块化函数编程及流程图

3.3 PQ算法模块化函数编程及流程图

(1)导纳矩阵生成模块：根据网络拓扑结构计算出导纳矩阵;

(2)根据功率误差公式计算出各节点功率误差的模块;

(3)生成修正方程系数矩阵的模块;

(4)高斯消去法解 修正方程式的模块;

(5)高斯消去法解Q-V修正方程式的模块;

(6)修正各节点电压值的模块。

流程图见图2。

3.4 算法编程细节问题说明

初始电压用“平启动”方式，即e=1.0,f=0.0给出;用高斯消去法解修正方程式;NR法雅可比矩阵的形成与迭代同步进行，即每次迭代时系数矩阵都将不同。对高压电力系统，雅可比矩阵中各行的最大元素是有功功率误差量对电压的横分量e的偏导数与无功功率误差量对电压的纵分量f的偏导数，它们都不在对角元素位置。为减少计算过程舍入误差，程序通过对调雅可比矩阵中奇数行和偶数行的位置来实现最大元素放在对角元素位置上，以提高计算精度;对PQ分解法将BX法应用于程序编写。修正方程式的系数矩阵在每次迭代计算时都将固定不变，在电网拓扑结构数学模型的建立之初就已确定，与每次电压相量迭代结果无直接关系;由于Vector只能对一维向量进行存储，而矩阵相当于一个二维数组，就出现了如何将二维数组转化成一维向量的问题。对于一个i行j列的二维数组，可通过下面语句将其转变为一维向量：

vector Matrix;

for(i=0;i MatrixSize;i++)

for(j=0;j MatrixSize;j++)

Matrix[i* MatrixSize+j]=X[i][j];

其中，一维向量的大小即MatrixSize*MatrixSize，它等于二维数组X[i][j]中所有元素的个数(也就是矩阵的大小)。由此解决矩阵存储的问题;收敛条件可根据需要输入，当满足收敛性要求时计算结束。

4. 基于C++的两种不同算法的实验验证

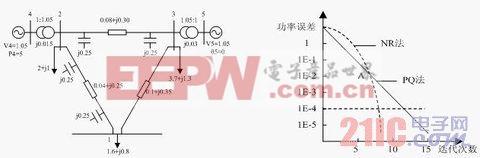
图3 包含5节点的网络模型算例 图4 敛代特性对数坐标比较

以图3的网络模型为算例，以 为收敛条件。用C++编程，使用NR算法的输出结果(直角坐标系)如表1，使用PQ算法程序的输出结果(极坐标系)如表2。

表1：NR算法程序的输出结果

表2：PQ算法程序的输出结果