DSP 在电源设计中的应用

0 引言

电源的信号测控部分由DDS信号发生和信号测量组成。DDS 在电源设计中的应用早已存在。在早期的DDS 设计中，硬件组成由计数器、触发器等多种多个分立逻辑元件组成; 而在出现可编程逻辑器件CPLD、FPGA 后，DDS 的硬件构成简化了许多。电源的信号测量，分为频率、幅值及相位的测量。频率的测量采用脉冲填充法; 幅值测量则随着A/D 转换器的采样速度及处理器速度的提高，由原来的有较大延迟的真有效值转换发展为周期实时采样计算;相位测量则在幅值测量的基础上，由原来的间相脉冲填充法发展为乘法器矢量测量。

DSP 的高速处理能力，使其可以实现DDS 中的CPLD 或FPGA 及测量电路中的模拟数字混合乘法器的功能，从而使电源的信号发生及测量的硬件设计更简单。

1 设计方案

方案设计如图1 所示。DSP 以等时间间隔快速、连续读取扩展程序存储器中的波形数据，送入并行高速D/A,并行高速D/A 即可输出预设信号波形。

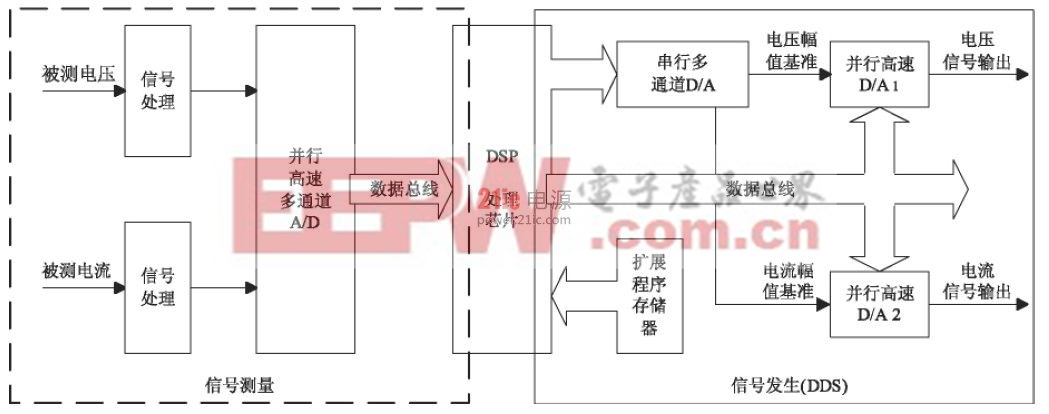
输出信号幅值的调整不如波形数据读取操作那么频繁，且对操作完成时间的长短、精度要求也不如波形数据读取高，所以选择串行多通道D/A.这样既可以降低成本，又可以简化部分硬件设计。以N 个波形读取时间间隔为计时基础，DSP 通过并行高速A/D 对经信号处理后的被测信号进行连续采样，通过计算，可得出被测信号有效值及相位。

2 DDS 的DSP 实现

2.1 DDS 原理

DDS 是利用相位累加原理直接合成所需波形的一种频率合成技术，典型的DDS 模型由W 位相位累加器、移相加法器、波形存储器ROM 查找表( LUT) 、D/A 转换器( DAC) 以及低通滤波器( LPF) 构成。其中相位累加器由W 位加法器与W 位累加寄存器级联构成。

DDS 工作时，每来一个时钟脉冲p,加法器将相位步进值Δθ 与累加寄存器输出的累加相位数据相加，把相加后的结果送至累加寄存器的数据输入端。

累加寄存器将加法器在上一个时钟脉冲作用后所产生的新相位数据反馈到加法器的输入端，以使加法器在下一个时钟脉冲的作用下继续与频率控制字相加。相位累加器输出的数据作为查表地址，从波形存储器( ROM) 中提取对应的波形抽样值( 二进制编码) ,送入D/A 转换器C 中。在相位累加器的数据输出范围0 ~ 2W – 1,与波形存储器中一个完整周期波形的地址，按照特定的函数关系对应起来的前提下，相位累加器的每次溢出，DDS 就相应的输出了一个周期的波形。因此，相位累加器的溢出频率就是DDS 输出的信号频率。由此可推导出DDS 输出的信号频率公式：fout = fclk × Δθ /2W

式中fout为DDS 输出频率; fclk为标准时钟脉冲，固定值; Δθ 为相位步进值，无符号整数，无单位; W 为相位累加器宽度。

从公式( 1) 可以看出，在相位累加器宽度W 为定值、相位步进值Δθ 为1 时，可得出DDS 的最小输出频率，即DDS 的频率分辨率fr.因此，只需要调整相位步进值Δθ，就可以使DDS 的频率以fr的整数倍输出。

2. 2 DDS 工作模式选择

根据公式( 1) 可以看出，在相位累加器宽度W 为定值的前提下，DDS 的输出频率，取决于Δθ 和fclk.

Δθ 取值为DDS 的相位分辨率时，DDS 输出信号的每个周期由固定点数组成，此时fout与fclk成比例关系，DDS 为调频模式; fclk为定值时，DDS 输出信号在单位时间内由固定点数组成，此时fout与Δθ 成比例关系，DDS 为调相模式。

调频模式，其关键点为采用锁相环技术对预置输出频率进行倍频[3 - 4].与调相模式相比，调频模式不仅要多出锁相环及相应倍频逻辑电路的设计，且在进行频率调整时，信号会有短时间的失锁，造成输出信号的振荡。因此，调相模式是本设计中DDS 的最佳选择。

2. 3 DSP 实现DDS 的优势

无论是用分立逻辑器件还是CPLD 或FPGA 设计DDS,其目的都是为了将相位累加器的累加、输出、波形数据查表等这些运算处理通过硬件电路高速实现。唯一的区别就是应用CPLD 或FPGA 设计DDS,可以将诸多分立器件实现的逻辑电路，通过VHDL 等编程语言编程固化在单一芯片上，从而达到简化硬件电路设计目的。而采用DSP 设计DDS,则完全可以利用其高速运算能力，通过软件编程来完成相位累加器的累加、输出、波形数据查表等运算。因此，相比于采用CPLD 或FPGA,采用DSP设计DDS 更灵活高效。

2. 4 基于DSP 的DDS 的参数设计

2. 4. 1 标准时钟脉冲fclk

的设计从公式( 1) 可以看出，在相位累加器宽度W 为定值、相位步进值Δθ 为1 时，可得出DDS 的最小输出频率，即DDS 的频率分辨率fr.因此，只需要调整相位步进值Δθ，就可以使DDS 的频率以fr的整数倍输出。

P = 2W ÷ Δθ

式中P 为DDS 输出信号的每个周期的组成点数。

将式( 2) 代入式( 1) ,可得：

fclk = fout × P

在P 足够多且每点波形数据分辨率与P 匹配的前提下，即可忽略DDS 信号输出的高频谐波含量，从而省略硬件设计中的滤波器环节，避免了由滤波器产生的相位偏移。当P = 10000 时，完全可以满足要求。如设计最大输出频率65Hz,可得fclk = 0. 65MHz.

fclk可利用DSP 计数器的中断产生。考虑到DSP 的工作频率均为MHz 的整数倍，所以fclk取值1MHz,更加便于中断的准确产生。

2. 4. 2 相位累加器宽度W 的选取

P = 10000 时，W 取值27 即可满足设计频率调节细度≤0. 01Hz 的要求。但相位累加值θ 在DSP 中定义为4 字节的操作数，W 取值27 时，DSP 需对相位累加值进行上限判断处理后再提取波形数据，从而产生细小的波形畸变并增加一定的运算量。考虑到可利用操作数的自然溢出来减少DSP 的判断及运算操作，所以W 取值32.

2. 4. 3 周期波形点数P 的选取

在不考虑四舍五入取值的前提下，相位累加器的输出值与波形数据表数组下标的函数关系如下：

A = P × θ ÷ 2W

式中A 为波形数据数组下标; P 为波形数据点数; θ为相位累加器输出值。

由于DSP 中没有现成的除法指令，除法是靠被除数与除数之间的移位相减来实现的，采用该函数的算法将增加DSP 的运算量。因此，可以通过事先将P ÷ 2W 作为系数，减少求数组下标运算步骤。但P ÷ 2W 可能为小数，如果取整计算，将使下标出现跳跃性变化，导致输出波形畸变增大。不取整计算时，如使用定点DSP,虽然价格便宜且运算速度较快，但会增加系统运算量。而使用浮点DSP,运算速度较慢且硬件费用会有相对提高。考虑到DSP 要进行多线程的任务工作，需要较快的运算速度，因此选用定点DSP,并对波形数据数组下标的算法进行进一步的改进。

将公式( 4) 中P 的点数由相位调节细度要求的最低点数Pmin调整至大于Pmin的最小的2 的X 次幂。

将P 代入公式( 4) ,简化得：

A = θ /2W-X

在DSP 中，所有的值都用二进制来表示。所以，在公式( 5) 里所有变量的取值均为无符号整数的前提下，A 的获得就简化成了对θ 进行( W – X) 次的右移。