NX-Nastran在零件结构改进中的应用
本文通过对失效零件的结构断裂问题进行研究分析,在实际设计空间以及成本的限制条件下,探寻合理的优化结构,找到工程中易实现、较经济的解决方案。
本文引用地址:http://www.amcfsurvey.com/article/165310.htm一、问题的提出
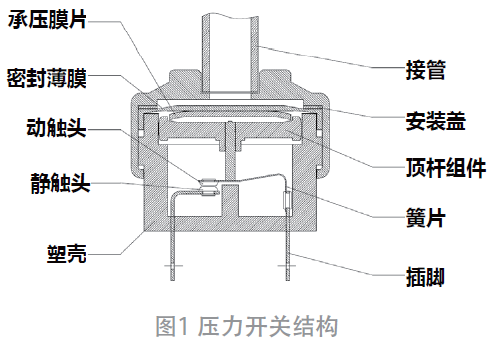
在新产品的研发中,对结构的可靠性需要进行批量的寿命测试。对如图1所示的零件进行批量的寿命测试中,在百分之一概率的样品中,凸起柱状结构a处出现了断裂现象,导致全套机构功能失效。图2为零件失效结构断裂状态。


分析此结构的工作状态,如图3所示,柱状结构表面受到金属零件周期性的压力F,压力F的大小可以通过测力计得到。在实际的使用操作中,柱状结构a处还要受到小幅冲击力以及工作状态中的环境温度与湿度影响。在针对问题的分析中,结合工程经验得出压力F是导致断裂的主要影响因素,为此可以简化条件,根据主要原因得到抽象分析模型(见图4),然后进行Nastran分析。
二、基于有限元Nastran分析与优化
1.结构应力集中分析
应用有限元分析软件Nastran的分析流程,首先对模型简化,进行现有结构的应力变形分析,找到造成断裂的结构应力集中位置,然后进行下一步的结构优化。
定义材料属性,用3D mesh 10节点单元对非规则性的模型进行网格划分,为了保证计算的准确与精度,进行局部的网格细化。设定合理的边界条件,对实际状态分析后施加有效均布载荷F ;选择结构静态线性求解器进行求解,抓住主要因素快速找到问题所在。在实际情况下造成断裂有多种因素,若用非线性求解器则会造成计算的复杂性,难以快速找到解决方案。如图5所示为网格划分结果及设定施加载荷位置示意;图6为应力集中的分析结果。由分析结果可知,柱状结构中1区位置处存在应力集中,需要针对受力的状况进行结构上的加强,同时确保柱状结构周边其他零件的运动不受影响。
 2.基于工程应用的结构优化
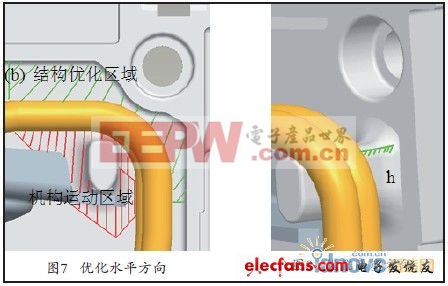
2.基于工程应用的结构优化首先确定工程条件下可优化的区域。对结构的优化必须保证不干涉到机构零件的正常运动,在实际可允许的范围内进行结构的改善。本文中要测量工作状态下运动机构(见图7) 需要的区域,从而找到可进行结构优化的区域,仅能在此限定范围内进行结构的优化。在模型中标示出图7优化区域的水平方向,图8为高度h方向上不干扰机构运动的限定范围。
其次确定可实现的优化目标。在确保柱状结构不断裂的强度要求下,尽量减少改变的结构,不但能减少模具改动的工作量与费用,而且节约原材料。
根据力学基本理论,在施力面相同的条件下,施加载荷与应力成正比。通过实验测试,失效样品中柱状结构能承受的平均压力为9N,大于此压力,结构的应力增大,断裂发生的机率增大。
在实际工作条件下,经测试此柱状结构需要承受12~13N 的平均压力,所以超过其所能承受的应力极限会发生断裂。这需要通过结构的改善来降低应力提高结构的强度,当施加载荷13N时,保证应力在极限范围内,就可以达到结构强度要求。计算载荷为9N条件下的应力分布,如图6所示,此计算结果5.858MPa为优化的极限应力目标值,即优化后的结构应力需接近目标值。
再次确定结构优化的思路,以理论为基础、工程经验为指导进行结构的改进。
根据材料力学理论,
,在载荷施加状态不变的情况下,增大抗弯截面模量
可以降低应力。分析柱状结构截面,使中性轴的位置偏近施力点,可增大抗弯截面模量;增加底部厚度,减小应力集中。具体结构尺寸的优化可通过软件计算,比较各种不同分析结果后得到较为优化的方案。
在载荷为13N的条件下,对结构进行优化,计算得到其应力分布结果。如图9所示,当载荷从9N增加到13N的情况下,原有应力集中区的应力值减小为3.717MPa。
如图10所示,通过结构的优化,消除了局部大应力集中存在的现状,最大应力区在载荷增加30%的情况下,应力值略小于优化目标值,为5.835MPa。说明结构强度有较大的增强,优化后结构可承受现有工作条件下的载荷。












评论