模糊滑模控制在跷跷板系统中的应用研究

1 引言
一般来说，大多数物理过程都具有复杂、高度非线性、易受外界干扰影响，且存在很大的不可知性等特点。利用传统的控制器来处理该类系统是非常困难的。然而，随着控制理论的不断发展，智能控制即使在不知道系统的数学模型的情况下也能获得比传统控制方法更好的控制效果[1]。跷跷板系统是一个比倒立摆系统更为复杂，更接近于实际应用的典型控制系统。它具有严重的非线性、强耦合、对干扰敏感、模型过于复杂等特点[2-5]。跷跷板系统是由一部小车、一个直流伺服电动机、两个分别用于测量角度和位置的电位计以及跷跷板三角体组成。而让跷跷板平衡的机制就是利用跷跷板系统中小车的移动来完成平衡的目的^[6]。
由于跷跷板系统具有高度的非线性和强耦合性等特点以及变结构控制的抖振问题，本文将模糊滑模控制算法引入系统控制中以柔化控制量。使用模糊控制策略不仅可以使控制系统滑动模态的品质得到保证和改善，同时消除了滑模控制中的抖振现象。
2 跷跷板系统的数学模型
跷跷板系统示意图如图（1）所示。

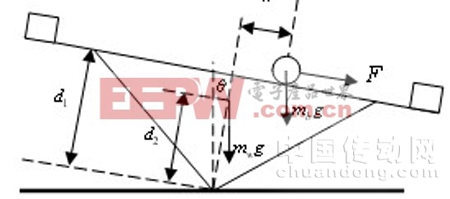
图（1）跷跷板系统示意图

图中各参数定义如下：
杠杆的倾斜角度；X : 小车的位置；d₁ : 杠杆相对支点高度0.125 m；d₂ : 杠杆中心点相对支点高度0.058 m；I_w : 转动惯量0.395kg.m²；m_b : 小车的质量0.57K；m_w : 杠杆的质量3.6K； : 重力加速度9.81N/K。
定义拉格朗日算子
L=T-U （1）
其中T 为系统的动能，U 为系统的势能。取状态变量为 ，为构造拉格朗日方程，分别求出

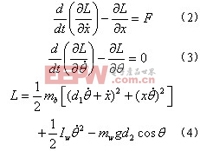
将（4）式代入（2）式和（3）式，即可得到（5）和（6）式

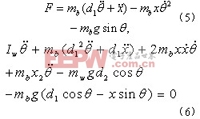
通过（5）和（6）式可分别求得 和 的表达式

方程组（7）即为系统的非线性状态方程表达式。

3 模糊滑模控制器的设计
滑模变结构控制具有响应速度快、鲁棒性强等优点，被广泛应用与非线性系统控制当中，但是滑模控制容易引起系统的抖振现象，导致系统的最终不稳定。模糊滑模控制是在不确定环境下，对于复杂对象进行有效控制的一种智能控制方法。它不依赖系统的模型，而且对干扰具有完全的鲁棒性，同时保持了模糊控制和滑模控制的优点。模糊滑模控制的基本设计方法是在滑模控制系统的趋近阶段通过模糊逻辑调节控制作用来补偿未建模动力学的影响，其目的是提高控制系统的品质、减少到达滑动面时间、降低抖振。文中利用模糊控制规则调整控制输入量 的大小，保证滑模控制到达条件得到满足。模糊滑模控制原理如图1所示。

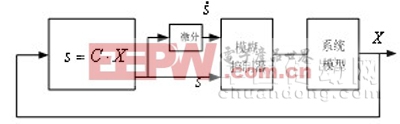
图1 模糊滑模控制原理图

由图可知，模糊滑模控制系统由三部分组成，即切换函数、模糊控制器、和被控对象。滑模函数的输入为系统状态变量，切换函数设计为s=C・X
（1）
模糊控制器的输入为切换函数 及其变化率 ，这样可有效的减少模糊规则的数量，很好的解决高阶系统多输入中存在的规则爆炸问题。控制的变化量 作为滑模控制器的输出，可使模糊滑模控制成为无模型控制，依赖于被控对象的程度较小^[7]。
根据模糊控制原理，定义模糊集 ，