基于直驱型PMSG风力发电系统的变桨自抗扰控制

摘要：为了实现大功率风力发电系统的恒功率控制，首先建立了基于直驱型PMSG风力发电系统的数学模型；其次，以功率偏差为控制器的输入信号，设计了一种基于自抗扰算法的风力发电系统变桨距控制器。最后，在阵风叠加随机风的作用下进行仿真研究。仿真结果表明，该控制器能够有效地控制桨距角，可以实现额定风速以上时系统输出功率的恒定。
关键词：风力发电系统；恒功率；自抗扰；变桨距控制器

0 引言
风能作为一种清洁的可再生能源，越来越受到世界各国的重视，风力发电是风能最常见的利用形式。永磁同步风力发电系统不需要励磁装置，具有重量轻，效率高，可靠性好的优点。风力发电机组由最初的定桨距型发展到变桨距型，从转速固定的变桨距型发展到目前技术最为先进的变速变桨距型，发电效率在显著提高。特别是变速变桨距机组，其发电机中采用的变速恒频技术提高了风力发电机组在低风速情况下的出力水平。采用永磁式发电机的直驱风力发电系统，无需外部提供励磁电源，把永磁发电机变频的交流电通过变频器转变为电网同频的交流电，做到风力机与发电机的直接耦合，省去齿轮箱，大大减小了系统的运行噪声，提高了可靠性，降低了系统成本，成为当前风力发电的研究热点。直驱型PMSG风力发电系统的关键在于额定风速时的变桨距控制。变桨距风力发电机组的桨距参考值可由风速、电动机转速和发电机输出功率3个参数来独立控制。文献提出一种由桨距角大小来调节控制器增益的控制策略，即在原有PI控制系统中加入一个增益调整控制器。由于PI控制器缺少微分调节作用，系统的动态性能受到一定影响。文献设计了模糊PID控制器对桨距角进行控制。输入信号的误差为e和误差变化率为ec，运用模糊推理，自动实现对PID参数的最佳调整，以满足不同时刻的e和ec对PID参数的自整定要求，从而得到桨距角变化目标的最佳调整。模糊PID控制器系统设计的核心为模糊控制规则设计，根据工程人员的实际操作经验和技术知识得到。本文设计了一种基于自抗扰控制算法的控制器，该控制器的参数调整可不依赖于实际经验，并能获得更好的控制效果。仿真结果验证了控制方法的有效性。

1 直驱型PMSG风力发电机组建模
1．1 风轮机模型
根据贝兹理论，风轮机产生的机械功率为：

式中：ρ为空气密度；Rt为风力机风轮半径；v为风速；Cp(λ，β)为风能转换系数，是叶尖速比λ和桨叶节距角β的函数；叶尖速比λ为风轮叶尖线速度与风速之比，即；Ω1为风轮的机械角速度。
风轮机产生的风力矩：

式中：CΓ(λ，β)为转矩系数，CΓ(λ，β)=Cp(λ，β)／λ。
在额定风速以下时，桨距角β为常值0。在额定风速以上，风能转换系数满足以下函数关系：

1．2 PMSG模型
在分析永磁同步电机的基本电磁关系时，假定永磁同步电机为理想电机，即满足：
(1)忽略铁心磁饱和的影响，不计涡流及磁滞损耗；
(2)永磁材料的电导率为零；
(3)转子上没有阻尼绕组；
(4)定子三相对称，感应电动势为正弦。
此时经过帕克变换后，在d-q轴坐标系下，PMSG的数学模型如下：

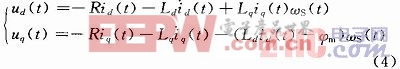
式中：R为定子电阻；ud(t)，uq(t)为d轴和q轴的定子电压；Ld，Lq为d轴和q轴的定子电感；φm为永磁体产生的磁通；转子旋转的电角速度ωs(t)=p×Ωh(t)，d-q轴坐标系以电角速度ωs(t)随转子一同旋转。
PMSG的电磁转矩为：