基于前馈控制的双馈感应电机矢量控制

摘要：基于双馈感应电机(DFIG)的五阶数学模型，建立了以电网侧电压和转子电流为控制量的简化数学模型。在此基础上分析了电网电压波动时的定子暂态电流的变化机理，提出一种转子电流前馈控制策略，通过转子阻尼电流消除电网电压波动引起的定子输出电流波动，从而提高DFIG的动态性能。实验结果证明了所提控制策略的正确性和有效性。
关键词：感应电机；矢量控制；前馈控制

1 引言
在风力发电系统中，基于DFIG的变速恒频发电系统占据很大的比例，因此深入分析和研究双馈式风力发电系统并网控制问题对提高风力发电系统的性能及效率有重要的意义。
近年来，各国学者对双馈风力发电系统正常工况下的运行机理及控制方法进行了较完善的研究。文献提出基于电网电压定向的矢量控制
策略，实现了转子电流有功分量和无功分量的解耦控制；文献基于DFIG电网电压定向控制，选取定子侧输出有功和无功功率为直接控制目标。
传统DFIG矢量控制是基于DFIG五阶数学模型设计的，通常利用转子电流闭环构成，且将定子侧电压视为常量。在此基于一种简化的DFIG
模型，考虑转子电流和定子电压两个变量，分别构成含反馈控制和前馈控制的矢量控制系统，提高了并网运行效果，且增强了抑制电网波动的能力。

2 双馈感应电机数学模型
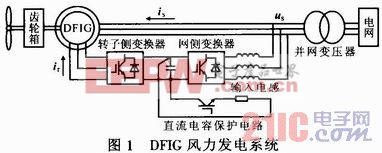
利用交直交变频器励磁的DFIG风力发电系统如图1所示。DFIG转子侧通过交直交变频器进行励磁控制，定子侧通过并网变压器接入电网。通过对DFIG转子电流进行适当的励磁控制，可以实现DFIG的变速恒频发电。后面讨论的DFIG稳态运行状态均采用该方法。

在同步旋转d，q坐标系下，DFIG的数学模型可表示为如下微分方程组：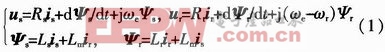

式中：us，ur和is，ir分别为定、转子电压、电流矢量；ψs，ψr分别为定、转子磁链矢量；ωr为转子角速度；ωe为电机同步转速；Ls，Lr分别为定、转子电感；Lm为互感。
由DFIG的数学模型可见，定转子各电磁物理量之间互相耦合影响。定子电流同时受转子电压和定子电压的影响。

3 基于前馈控制的转子励磁控制
分析DFIG数学模型，将定子磁链方程代入电压方程，可得：

由于定子侧电阻相比定子阻抗很小，故可略去以及RsωeLm。同时在采用电网电压矢量定向控制中，d，q坐标系中的d轴与定子电压矢量方向保持一致，定子电压q轴分量可认为是零。基于以上简化原则，可将式(3)化简为：

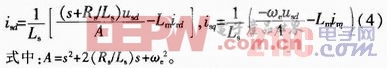
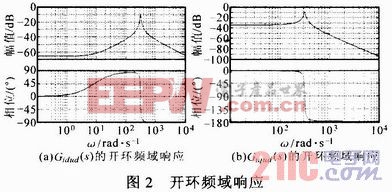
从以上分析可知，由转子电流和定子电压至定子电流的传递函数共有3个，分别为定子电压至转子电流传递函数Gidud(s)和Giqud(s)、转子电流对定子电流的传递函数Gisir(s)，其中Gisir(s)为常数，Gisir(s)=Lm／Ls。图2示出开环频谱。

式(5)表明，由定子电压至定子电流的传递函数是一个二阶环节。因此，当电网电压出现一定波动时，电网电压的变化将引起定子电流产生一个工频周期振荡分量，该振荡分量将引起定子侧输出功率的振荡。

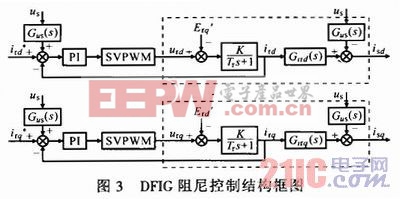
因此，通过在转子电流中引入一个与电网电压振荡分量相反的参考值恰好可对由电网电压波动引起的定子电流振荡形成阻尼作用。令：

转子电流的参考值将由功率控制外环产生的电流给定值ird有功，irq无功与暂态阻尼电流irdd，irqd共同组成，即irdref=ird有功+irdd，irqref=irq无功+irqd。加入阻尼控制后的系统等效控制框图如图3所示。

4 实验
针对该前馈控制策略，设计了一套系统结构如图1的DFIG实验系统。系统中双PWM变换器的逆变级和整流级均以PM75RLA120型IPM为主体构成。控制系统以TMS320F2812微处理器为核心构成，实现双PWM变换器的控制、通讯与保护功能。DFIG参数为：定子额定电压380 V，额定电流6．8 A，转子侧额定电压380 V，额定电流3．2 A，极对数为2，额定转速1 800 r·min-1，定子电阻1．37 Ω，转子电阻1．65 Ω，定子电感0．161 H。DFIG由一台三相异步电机驱动。
实验中，DFIG转速为1 600 r·min-1，基于前馈控制的DFIG定子侧电压电流如图4所示。

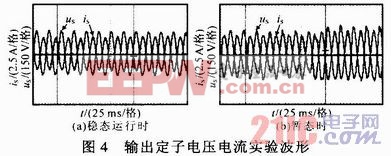
图4a为稳态运行时波形。此时DFIG定子侧稳定输出有功功率2 kW。图4b为有功功率给定值变为3．6 kW的动态过程。可见DFIG定子侧输出能很好地跟踪参考信号，系统动态响应快速，且在电网电压由于有功输入增加而出现一定波动时定子电流控制获得了良好的稳态特性。

5 结论
在双馈感应电机的简化数学模型的基础上，分析了电网电压波动与定子电流工频周期振荡分量之间的关系，提出在转子电流控制中引入前馈控制，即在转子电流的参考信号中加入增加系统阻尼的阻尼控制方法，以消除电网电压波动对定子输出电流的影响，提高系统的动态响应。给出双馈感应电机控制系统的稳态和动态实验结果，验证了所提控制策略的正确性。