小波在扩频通信中的应用

本文描述了基于正交小波函数族的多址通信原理，并提出了一种多速率正交小波调制方法.用具有不同伸缩尺度的小波函数对不同信道中的码流进行编码，可以达到扩展信息序列频谱的目的，因此这一多址技术具有很好的抗干扰性能.本文还讨论了这一多址方式的其它特点，并针对信道容量不平等问题提出了一些解决办法.
　　关键词:小波；多址通信；调制；扩展频谱

The Applications of Wavelet in Spread Spectrum Communications

WU Hao,SONG Wen-tao,LUO Han-wen
(Dept.of Electronic Engineering,Shanghai Jiaotong Univ.,Shanghai 200030,China)

　　Abstract:The principle of multiple access communication is described,which is based on the orthogonal wavelets in this paper.And a multirate orthogonal modulation scheme is proposed.The goal of spreading information sequence spectrum is met by coding bit-streams with the different scaled wavelets.So this multiple access technology has a good performance in resisting narrow jam and interference.The other characteristics are also discussed.Some methods are given to resolve the inequity of the channel capacity.
　　Key words:wavelet;multiple access communications;modulation;spread spectrum

一、引　　言
　　近年来，小波分析方法在信号检测、多尺度边缘提取、语音及图像处理等诸多通信领域得到了广泛应用［7，8］.在扩频通信领域中，基于正交小波函数族的多址扩频技术也被提出［1］，并被称为SDMA(scale-division multiple access，尺度划分多址).现在广泛应用的CDMA技术是利用伪随机序列来进行扩频，所得到的近似正交的伪噪声序列具有很强的抗窄带噪声的性能；而SDMA则利用正交小波函数族来完成扩频，同样具有类似性能.但是，在CDMA系统中，信息都是在同一频段上传输，窄带噪声会污染整个信息流；而在SDMA系统中，信息被分配到不同子带上传输，窄带噪声只会污染部分信息流，因此，SDMA的系统性能要优于CDMA.下面将分别阐述SDMA的原理、调制解调模型和SDMA的特点，最后给出结论.

二、SDMA扩频原理
　　小波分析的基础理论为寻找合适的正交小波函数族提供了强有力的理论依据，也是SDMA的数学基础.小波函数定义为

　(1)

式中w(t)称为基本小波.实际应用中，通常采用进二小波，定义为

ψmn(t)2m/2ψ(2mt-n)　(2)

　　根据小波函数性质，有ψmn.ψkl>=δm,kδn,l，其中δi,j=对任意信号x(t),其离散二进小波变换及反变换为

xmn=∫+∞-∞x(t)ψmn(t)dt　(3a)
　(3b)

　　现在考虑M条二进制码流sm∈{0,1}，m=1,2,…,M,对于在L2(R)上的正交集ψmnT,可将sm合并为

　(4)

其中n表示一个序列的第n个比特，T是一个比特的持续时间.因此，在接收端信号的解调就是根据(3b)对c(t)进行小波变换以提取序列sm.下面从式(4)出发来推导c(t)的功率谱表达式.
　　c(t)的自相关函数为

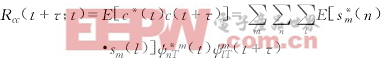
假定信息序列{sm(n)},m=1,2,…,M，是广义平稳过程，其自相关函数定义为Rss(k)=E［s*m(n).sm(n+k)］，所以

因为c(t)为广义周期平稳过程，故有

　(5)

从式(5)的傅立叶变换得到c(t)的功率谱密度表达式

　(6)

其中,并定义信息序列的谱密度为

代入式(6)就得到Φcc(ω)的进一步表达式

　(7)

从式(7)可以看出，信息序列经过小波变换编码后，其频谱得到了扩展，并且扩频系数η=2m,m＞0.可见，各信道的扩频系数是不相同的.

三、基于SDMA的调制解调模型
　　根据多分辨率分析理论，信号c(t)的调制与解调就是小波重构与分解过程.为此，引入另一个函数φ∈L2(R)，且有φmn(t)=2m/2φ(2mt-n)，使得分别以ψ和φ为基的两个空间相互正交，则存在两个序列{p(n)}和{q(n)}使得

　(8a)
　(8b)
　(8c)