射频功放的建模

标签：射频电路 模糊逻辑

随着通信技术的发展，射频电路在通信系统中得到了广泛的应用。功率放大器的研究和设计一直是通信发展中的重要课题。近年来，基于模糊神经网络的射频器件和电路建模的研究取得了巨大的成果，对大规模集成电路和复杂电路的建模有着巨大的启发意义， 成为当今研究的热点之一，本文将基于这个理论对射频放大器进行建模和研究。

1 建模方法的介绍

本文将采用模糊逻辑网络中的一阶Sugeno模型， 为了实现Sugeno 模糊推理系统的学习过程， 一般将其转化为一个自适应网络，即自适应模糊神经推理系统， 如图1所示。

该自适应网络是一个多层前馈网络， 它可以分为5层， 其中的方形节点需要进行参数学习。下面分别介绍这五层。

图1 自适应模

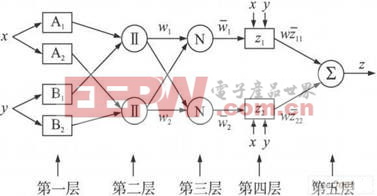
糊神经推理系统结构

第1层 计算输入变量的匹配度， 即模糊化过程。假设模糊集采用高斯函数，那么该层输出( Oi表示第j层的第i个输出)为:

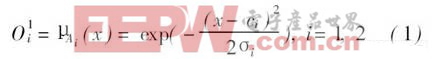
对y 的计算同理， ci， σ i 分别表示高斯函数的中心和宽度， 是模糊规则前提条件中需要调节的参数。

第2 层 计算当前输入对各条规则的激励强度，采用对规则前件部分各模糊变量的隶属度作乘积运算， 即:

第3层 对激励强度进行归一化:

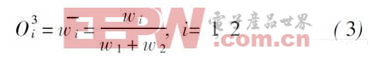
第4层 计算每条规则的输出， 一条规则的输出是给定输入对该条规则的激励强度与结论部分的乘积:

第5层 计算模糊系统的输出， 总的输出是所有规则输出之和:

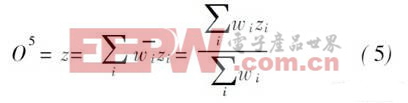
由此可见这一模糊逻辑系统定义了从x、y 到z之间的一个映射:

通过对模糊规则中各参数的精心选择， 可准确地刻画变量之间的关系。

用 模糊逻辑建模可以把整个建模过程分成两步: 初始模型的建立和模型的后续训练调整。初始模型的建立除了可根据该领域已有的一些经验、知识外，现在还可以根据一组训练样本数据，运用一定的算法确定输入变量与输出变量的模糊集个数与相应的隶属度函数的形状， 及一组模糊规则。有了这样一个初始模型后，再用学习算法，如BP算法、DFP算法，来调整隶属度函数中的参数， 逐步减小系统的模糊输出值跟实际输出值之间的误差，可取得较好的效果。

2 建模过程

在下面的实例中应用ANFIS进行建模的步骤如下:

( 1)在ADS中对设计好的功放电路进行仿真，这里分别对输入为单音信号、双音信号以及调制信号的功放电路进行仿真，最终目的是建立一个描述输入输出端口关系的行为模型，故选择输入和输出的电压数据用以训练之用。

( 2)编写程序， 预设ANFIS中的参数值， 确定隶属度函数的类型、模糊规则的条数、迭代次数、模糊集的个数等，建立初始模型，并完成对训练数据的学习;( 3)利用检测样本数据检验所建立的模型; 采用最小二乘法和梯度下降法对模型的参数进行调整。

( 4)观察检测结果， 若检测误差满足精度要求，建模结束， 若不满足， 继续调整。

本 文采用一个三输入单输出的初始模型， 输入变量选为Vin ( k )， Vin ( k- 1)， Vout ( k- 1)三个输入变量， 其中Vin ( k ) 为输入电压， 变量Vin ( k - 1 ) 用Vin ( k- 1) = Vin ( k ) - Vin ( k - 1)的差分形式来替换。Vout ( k- 1)为考虑记忆效应而加入的项，即前一刻的输出量。输出变量为一单变量Vou t ( k )。这样可以将整个需建模的电路输入输出的动态关系用式( 7)予以表达:

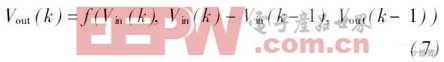
模型采用高斯隶属度函数， 模糊规则条数为[ 2 12]， 共四条， 采用平均分割法。

3 应用实例

以下是一个基于SM IC 技术设计的射频功率放大器，如图2所示。它的设计指标如下:

S11 - 15 dB， S21> 20 dB， P1 dB > 20 dBm，PAE 30% ， Pgain > 20 dB。

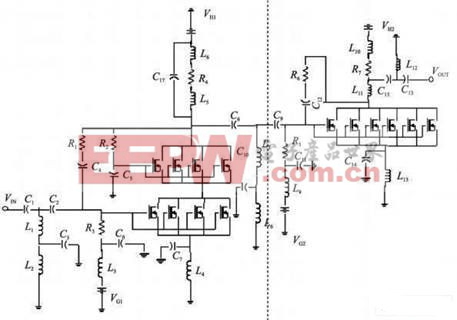
图2

电路中选用SM IC 库中的NMOS管， 其他元件参数如表1~ 3所示。

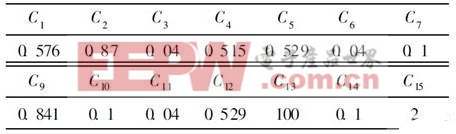
表1 元件参数单位: pF

表2 元件参数单位: nH

表3 元件参数单位: kΩ

电 路工作在2. 45 GHz下， 输入功率为RF_input= - 20 dBm~ 10 dBm(间隔1 dBm)的信号，对电路进行HB仿真， 并选取时域下两个周期的抽样输入输出电压抽样数据作为训练数据。检验数据的选取与上述类似，可以选择输入功率RF_input= - 19. 5 dBm~10. 5 dBm (间隔为1 dBm )内的一组或多组信号。