基于DSP数字振荡器的移相正弦波发生器设计

0 引 言
产生数字式移相信号的方法有很多。传统的直接数字频率合成(DDS)移相原理是先将正弦波信号数字化，并形成一张数据表存入两片ROM芯片中，此后可通过两片。D／A转换芯片在计数器的控制下连续地循环输出该数据表，就可获得两路正弦波信号。当两片D／A转换芯片所获得的数据序列完全相同时，则转换所得到的两路正弦波信号无相位差。当两片D／A转换芯片所获得的数据序列不同时，则转换所得到的两路正弦波信号就存在着相位差。相位差的值与数据表中数据的总个数及数据地址的偏移量有关。这种处理方式的实质是将数据地址的偏移量映射为信号间的相位值。数据的偏差可以通过外部微处理器来获得相应的数字量输入，这个数值对应着正弦信号的移相角度。直接频率合成方法具有频率转换时间短、相位噪声性能好、精度高，产生的信号频率范围宽等优点，但由于需要采用地址、相位计算、访问存储器操作等环节，导致直接频率合成器结构复杂、成本高、移相分辨率低。本文利用DSP技术，通过数值迭代方法，即用DSP数字振荡器的实现原理获得两路正弦波信号。通过仿真，硬件实现，能得到设定参数的两路正弦波输出，达到了设计目的，并具有调整方便灵活、分辨率高等特点。数值迭代方法能精确计算角度的正弦值，只需较小的存储空间，选择正弦周期中的样点数、改变样点间的延迟，能产生不同频率的波形，可利用软件改变波形幅度及相位。

1 波形及移相波形发生器的DSP实现原理
利用DSP通过运算，用叠代的方法产生正弦信号，即数字振荡器。数字振荡器的单位冲击响应为sin(nωT+θ)・u(n)即系统在δ(n)的激励下，产生振荡，输出相位为θ的正弦序列，该系统的系统函数就是冲击响应的Z变换，即

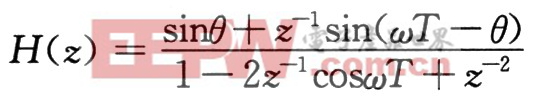
则该系统所对应的差分方程为

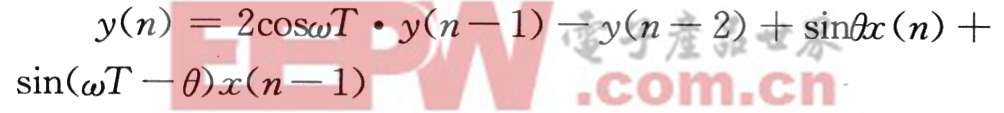
通过叠代可由差分方程求出系统的冲击响应。系统的输入为x(n)=δ(n)，初始条件为零。则由差分方程可得：

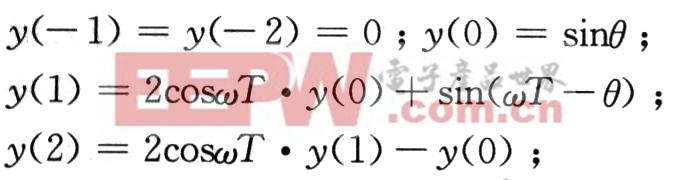
当n≥3时有：y(n)=2cosωT・y(n－1)－y(n－2)。在n≥3以后，y(n)能用y(n-1)和y(n-2)算出，这是一个递归的差分方程。因此得到如下结论：只要已知系统输出正弦信号角频率ω和采样周期T就可以得到系统差分方程，系统只需每隔T秒时间计算一次差分方程，就可得到当前正弦采样序列y(n)的值。设定的y(1)、y(2)初值不同，初始相位就不同。在设计中，主程序通过键盘输入频率及相位差等数据，在初始化时依输出信号频率、采样速率及相位差等数据先计算出两路正弦信号的初始值y1(1)、y1(2)和y2(1)y2(2)，然后开放定时器中断。以后每次进入定时器中断服务程序时，利用前面的y1(1)、y1(2)和y2(1)y2(2)，计算出新的y1(0)和y2(0)。虽然两次计算并输出y1(0)和y2(0)有一定的延迟，但由于DSP的高速流水线运行及McBSP高速串行输出，所引起误差将很小。