基于MATLAB在FPGA 算法上浮点定点转换的实现

浮点定点转换是在 FPGA 上实现算法时最困难的地方（图 1）。

虽然 MATLAB 是一种强大的运算开发工具，但其许多优点却在浮点定点转换过程中被降低了。例如，由于定点算术中精度较低，新的数学误差被引入算法。您必须重写代码，使用能够反映实际硬件宏架构的低级模型来替换高级函数和运算符。而仿真运行时间将可能长达 50 倍之久。基于这些原因，MATLAB，这一算法开发的优势选择，却经常遭到遗弃，转而使用 C/C++ 进行定点建模。
　　
生成定点模型
　　
如果未将高级函数和运算符替换为硬件精确的宏架构，浮点 MATLAB 算法的定点表示将不会真正反映最终硬件的响应（图 2）。

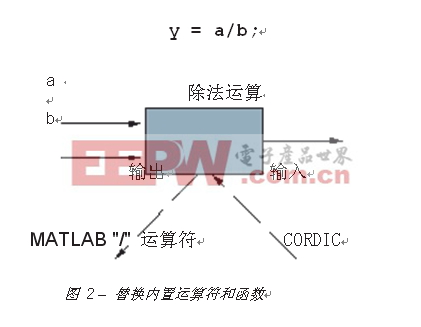
图 3 对此进行了突出显示，该图使用一组量化为 8 位有符号二进制补码的随机输入矢量，对 MATLAB 除法运算符与工具硬件 CORDIC 除法算法的定点响应进行了比较。

　　
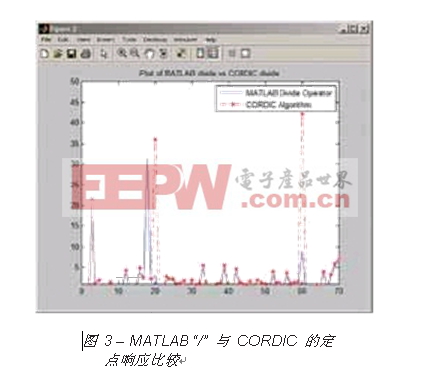
根据数据数值，计算输出之间将存在巨大分歧。
　　
在定点生成过程中，AccelDSP™ Synthesis 综合工具的 IP Explorer™ 技术将自动使用硬件精确的表达式替换高级 MATLAB 函数和运算符（图 4）。此步骤是透明的，且不需要对 MATLAB 代码进行修改。您可以使用综合指示来重新定义初始宏架构和微架构选择。

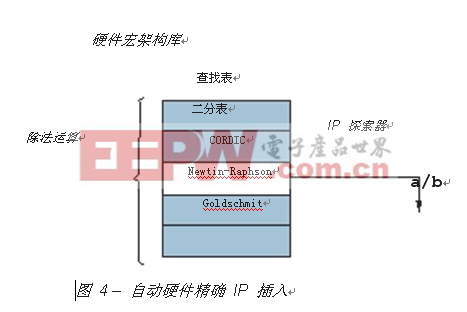
一旦这些运算符替换为硬件精确的宏架构，量化过程就将开始。
　　
图形辅助式自动量化
　　
与定点 DSP 处理器不同, FPGA 结构允许使用可变定点字长。通过解除对变量的固定 16 位或 24 位边界限制，您可以执行需要位数增长的算术计算而不会引起额外的数值误差。
　　
这对于像雷达、导航和制导系统等要求较高数值精度的应用来说是一个巨大的优点。
　　
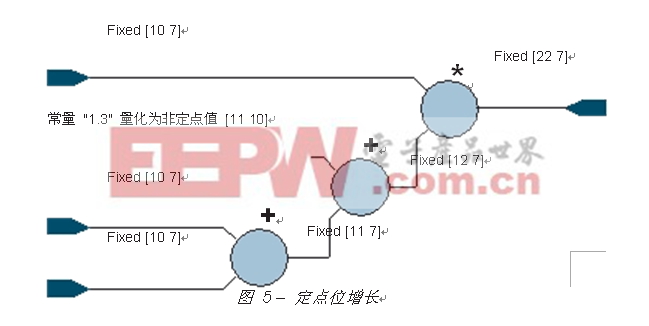
在大多数情况下，位增长率定律 (bit growth rules) 是简单直接和易于理解的。例如，一次加法的结果增长一位，而一次乘法的结果则增长到等于输入字长度的总长度（图 5）。然而，要在实际设计中确定变量的这些属性，将是一个高度反复的过程。允许未检查的位数增长现象发生，在硬件中代价是昂贵的，通常也是不必要的。如果您技术功底深厚，您可以采用各种技巧来尽可能地减小字长而同时保持数值精度。