基于双混沌映射的图像加密算法研究
随着信息技术的发展,图像保密技术将在越来越多的应用场合受到重视。由于图像加密具有数据量大、相邻像素间相关性强等特点,一些传统的加密算法并不适合于加密图像信息。虽然利用传统的加密技术对图像加密是可实现的,但其加密效率低、安全性不高,不能适应图像加密的需要,因此专用的图像加密技术被广泛关注。近年来混沌理论的应用研究引起了密码学界的关注,由于混沌遍历性正符合Shannon提出的密码系统设计的扩散混淆等基本原则,使混沌理论在图像加密中得到广泛应用。本文提出一种基于Logistic和Henon双混沌的图像加密算法,并通过实验分析证明,该算法具有优异的加密性能和运算效率。
本文引用地址:http://www.amcfsurvey.com/article/150587.htm1 混沌理论及模型
混沌是非线性确定系统中由于内禀随机性而产生的外在复杂表现,是一种貌似随机的非随机运动。基于混沌的保密技术已经涉及到数据安全及保密通信等众多研究领域,目前许多研究将混沌信号作为通信中的载波以对抗多径衰落,并具有一定的保密性。然而,无论采用载波同步解调还是非相干接收的通信方式,混沌载波通信所具有的保密性都已经受到了不同程度的威胁。在基于载波同步的混沌保密系统中,混沌同步特性容易被攻击者利用进行状态空间重构;对于非相干的混沌扩频系统,截获者可通过训练预测出各码元的时间窗口,并进行与权威接收端类似的差分解调。
混沌与密码学有着紧密的联系,一个好的密码系统应该具备以下几个条件:(1)把明文变换为尽可能随机的密文;(2)加密算法对明文有高度敏感性;(3)加密系统对密钥有高度敏感性。由于混沌具有对初值的敏感性、良好的伪随机特性、轨道的不可预测性等特征,这些特征正好能够满足密码系统的要求。
Logistic映射是一个非常简单却具有重要意义的非线性迭代方程,虽然它具有确定的方程形式,不包含任何不确定因素,却能产生完全随机的、对参数滋的动态变化和初值极为敏感的序列。其定义如下:

初始值极度敏感,对于相差的初始值,方程迭代出来的轨迹差别相差很明显,一般情况下,很难从一段有限长度的序列来推断出混沌系统的初始条件。该混沌模型迭代方程简单,混沌加密参数只有一个,这决定了其加密运算速度快,特别是比高维的混沌系统要快很多,但其密钥空间比较小,安全性稍差,因此不考虑单独使用它。
Henon混沌系统是1976年由Henon提出的一种二维迭代系统,具有两个参数的平面映射族。Henon混沌映射定义如下:

式中,a、b为控制参数,当1.05a1.8、b=0.3时,Henon映射处于混沌状态.当处于混沌时,它与Logistic模型同样具有混沌的特性,不同的是Henon映射是一个具有两个参数的平面映射族。虽然理论上对Henon混沌的研究比较成熟,但是由于其产生混沌序列的特殊性,一般也不单独使用。
2 加密解密矩阵的构造
由于单混沌存在诸多缺陷,密钥空间小,且在有限精度的系统下受限制,单混沌映射加密易受到攻击利用。因此,本文利用Logistic和Henon双混沌系统来构造加密矩阵实现对图像加密。首先对Logistic混沌系统产生的序列通过一种动态量化得到置换矩阵的随机数,对图像的像素位置置乱;再通过Henon混沌系统的映射,利用整数求余的量化方法来得到异或加密的随机数,与置乱后的图像依次异或.图像加密效果完全取决于两种混沌系统产生的随机数,因此,对Logistic混沌的动态量化和Henon的整数求余量化成为实现加密效果的关键。
设原始图像为I,大小为m×n,则图像I可以表示为:I=F(i,j)(0≤i≤m,0≤j≤n)。其中,(i,j)表示像素点位置,F(i,j)表示该点处图像的数据,则F(i,j)可构成图像数据矩阵T.





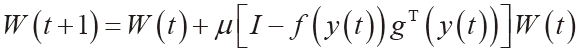




评论