RBF网络和贝叶斯分类器融合的人脸识别方法设计

引言

本文基于人脸图像分块和奇异值压缩，进行RBF 神经网络和贝叶斯分类器融合的设计。将人脸图像本身的灰度分布描述为矩阵，其奇异值特征具有转置不变性、旋转不变性、位移不变性、镜像不变性等诸多重要的性质，进行各种代数和矩阵变换后提取的代数特征是人脸的表征。由于整体图像的奇异值向量反映的是图像整体的统计特征，对细节的描述还不够深入，本文模拟人类识别人脸的模式，在图像分块和加权的基础上，突出待识别人脸的骨骼特征，近似于人类在识别人脸时自动剔除同一人脸的变化部位的差异能力

径向基函数（RBF）网络是一种性能良好的前馈型三层神经网络，具有全局逼近性质和最佳逼近性能，训练方法快速易行，RBF 函数还具有局部响应的生物合理性。RBF神经网络隐含层结点使用了非线性传输函数，比单层感知器网络具有更强的分类能力。在隐含层中心确定的情况下，RBF神经网络只需对隐含层至输出层的单层权值学习修正，比多层感知器具有更快的收敛速度，这也是本文选择RBF神经网络作为分类器的原因。

在 RBF 神经网络构建和初始化采取有监督的聚类算法，在网络参数的最终调整和训练方面采取 Hybrid学习（HLA）算法。在隐层参数固定的条件下，由线性最小二乘法计算隐层和输出层之间的连接权值，由梯度下降法调整隐层神经元的中心和宽度。这种混合学习算法，能使RBF网络逼近Moody准则下的最优结构，即：在没有其它先验知识的情况下，与给定样本一致的规模最小的网络就是最好的选择。从而保证该网络具有较好的泛化能力。

贝叶斯网络是一个带有概率注释的有向无环图，图中的每一个结点均表示一个随机变量，图中两结点间若存在着一条弧，则表示这两结点相对应的随机变量是概率相依的，反之则说明这两个随机变量是条件独立的。网络中任意一个结点X 均有一个相应的条件概率表（CONditional Probability Table，CPT），用以表示结点X 在其父结点取各可能值时的条件概率。若结点X 无父结点，则X 的CPT 为其先验概率分布。贝叶斯网络的结构及各结点的CPT 定义了网络中各变量的概率分布。

奇异值分解SVD

奇异值分解非常有用，对于矩阵A（m*n），存在U（m*m），V（n*n），S（m*n），满足A = U*S*V’。U和V中分别是A的奇异向量，而S是A的奇异值。AA'的正交单位特征向量组成U，特征值组成S'S，A'A的正交单位特征向量组成V，特征值（与AA'相同）组成SS'。因此，奇异值分解和特征值问题紧密联系。

奇异值分解提供了一些关于A的信息，例如非零奇异值的数目（S的阶数）和A的秩相同，一旦秩r确定，那么U的前r列构成了A的列向量空间的正交基。

对于任何一个矩阵A∈Rm×n，利用奇异值分解将其转化为对角矩阵。

设A∈Rm×n（不失一般性，设m≥n），且rank（A）=k，则存在两个酉矩阵Um×m和Un×n及广义对角阵Dm×m使下式成立：

其中U的列向量是AAT的特征向量，V的列向量是ATA的特征向量，T表示转置。

称为矩阵A的奇异值， ui（i=k+1,…,m）是AAT对应于λi=0的特征向量，vi（i=k+1,…, n）是ATA对应于λi=0的特征向量。如果矩阵A代表一幅人脸图像，则式

表示对该人脸图像进行了正交分解，将矩阵

中主对角线上的奇异值元素连同中剩余的（ri-k）个0组合构成一个n维列向量

。

由于任何实矩阵A对应唯一的奇异值对角阵

，因此，一幅人脸图像对应于唯一的奇异值特征向量。

（1）从人脸数据库选择人脸作为识别训练集；

（2）将被选入训练集的人脸图像几何归一化处理；将被选入训练集的人脸图像灰度归一处理；

（3）将预处理过的人脸图像划分成大小为的子块；

（4）将每一幅图像变为一个列向量（先分别将每一个子块所有向量排成一列，再将所有子块按顺序排成一列）；然后以子块为单位进行；

基于面部骨骼特征、眼睛的分布、鼻子的形状等结构特征，是鉴别人脸的主要依据。将每一幅人脸图像所形成的矩阵划分成…等个二维矩阵分别降维为一维列向量。求训练集中所有对应子块的平均值，

；再对每一类样本中的所有对应子块求平均，

；对应子块进行样本规范化，

；

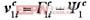并求协方差矩阵：

，

从中取 m 个较大特征值对应的特征向量，构成对应子块的特征脸空间 W1 ，即W1 =[w11,w12,…,w1 m ]T 。再对训练样本进行规范化处理

，投影到特征脸空间，获得投影特征为：

。对任一测试样本对应子块进行规范化处理，即

，然后得到投影特征，即

　用上述方法逐一对每个子块进行处理。得到

。

基于特征分块贝叶斯分类器设计

每个基于特征分块的贝叶斯分类器，利用了所对应的图像块包含的判别信息，为得到性能更好的分类器，需要将这些分类器融合给出最终的判别结果。可以有多种办法实现分类器融合，如加权求和、相乘等。本文采取加权求和的方法：

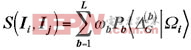
其中

表示两幅图像

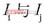
的相似度，L是贝叶斯分类器(FBBC)的总数（这里是9），

是与的第b个特征块之间的差值。

是由第b个贝叶斯分类器计算出的类条件概率密度。是第b个贝叶斯分类器对应的权值。

不同的特征块对应的贝叶斯分类器对最终判别结果贡献是不相同的，本文采取的是基于子分类器分类准确率分配权值的方法：将各子分类器重新放回其训练集，计算其在训练集上的识别率，利用这些识别率，采用下式计算第b个子分类器的权值：

图1人脸图像的预处理

图2 RBF神经网络的工作原理

RBF神经网络设计

直接利用matlab工具箱进行，这是一种较简单的设计方法，工具箱中提供了好几个函数可以利用，newrb、newrbe，newpnn，newgrnn,早一些的版本还有solverb等。这几个函数的使用以及参数说明请大家看相关资料。其中，为了看到每一步网络的性能函数变化，建议设置DF参数时设为1。这样每一步的图都可以显示出来，就对生成的网络的过程有一个清楚的认识。要查看设计好的网络的参数，中心采用net.IW{1},输出层权值采用net.LW{2}，隐含层的偏置利用bet.b{1},输出层的偏置采用net.b{2}进行察看。当然，修改的时候：例如要修改输出层的偏置，那么，就是net.b{2}=??,就可以了。这种方法网络的初始中心是随机从输入的训练样本中选取的，中心的个数也是由少到多逐步增加的。建议在确定spread参数时不要设计得太小，太小可能影响对测试样本的识别。我自己做的是模式分类，但是对于曲线拟合应该也是一样的。

利用聚类算法确定中心，可以利用的聚类算法较多，最普通的就是K—均值聚类算法，还有最近邻、模糊聚类、支撑向量基等方法，这些方法都是先确定中心，然后输出层权值以及输出层的偏置再采用lms、rls算法等进行确定。在设计时，偏置可以根据自己的需要来设计，可以有也可以没有。

假定∈（1≤j≤r）为输入层神经元，为隐层第 i个神经元的中心，则第j个神经元在第i个隐层节点的输出为： , i =1,2,…,u，式中||||表示欧氏范数。当RBF选用高斯核函数时，其输出为：

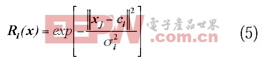
式中为隐层第 i 个神经元的宽度。输出层第 k 个节点的输出值 为： ，式中为隐层节点 k 到第 j 个输出节点的连接权值。

RBF神经网络的构建和初始化

RBF神经网络隐层聚类的初始化过程如下[10]：

（1）隐层节点数u=s。假设每个类收敛于一个聚类中心，再根据情况具体调整。

（2）隐层第 k 个神经元的中心为 k 类特征矢量的均值。，k=1,2,…,u，

（3）计算从均值 到属于类k 的最远点的欧氏距离

（4）计算各个j聚类中心到k聚类中心的距离，j=1,2,…,s, j≠k

（5） 包含规则：若且，则类k包含于类中，类应被

RBF神经网络的算法

网络学习就是通过调整连接权 、隐层中心和宽度，以减小输出误差。

1、连接权值的调整

定义误差函数为：

，

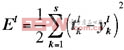
，其中

是第个训练样本的实际输出值和理想输出值。通过线性最小二乘法求解最佳权值。

2、隐层中心及宽度调整

W固定，采用梯度下降法，经推导可得和的迭代计算公式为：

其中，

分别为隐层中心

宽度的学习速率

，m为迭代次数。

实验结果及分析

利用Yale人脸库中的人脸图像数据进行实验人脸识别实验研究，将人脸图像分块加权重构的奇异值向量X1，X2，…，Xl（其l中为训练样本的数目）矩阵依次输入RBF神经网络训练，当满足误差容限或训练次数，停止训练。在测试过程中，依据竞争选择的办法做出识别判断。
本文重点研究人脸图像的32子块权值选取情况如下：

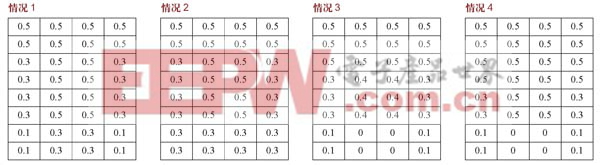
表1 人脸图像划分不同子块数的识别结果

表2 赋予人脸图像32子块不同权值的识别结果

实验结果表明，基于人脸面部骨骼特征、以及眼睛分布、鼻子形状等结构特征，是鉴别人脸的主要依据。通过子块权值的合理分布，突出人脸骨骼特征，而对嘴部和皮肤折皱等表情变化部分特征给予弱化或剔除，这与人类识别人脸时的模式相近，识别效果较好。但是，子块不宜过多，否则增加RBF神经网络计算负担，识别率也会有所下降。

结论

本文提出了基于图像分块奇异值压缩，融合RBF神经网络和贝叶斯分类器的人脸识别方法，模拟人类识别人脸时剔除同一人脸变化部位的差异能力，采用不同子块单独进行人脸识别，根据RBF神经网络识别效果进行权值分配，通过实验证明，本文方法在降维和识别率方面均取得良好的效果，在正面人脸部位（尤其是下颚部）变化较大时，具有良好的识别精度和识别速度。