全片内LDO频率特性的简化电路分析方法

　　摘要：对于无片外大电容的低压差线性稳压器来说，用建立小信号模型来分析系统传输函数从而推出零极点分布的方法过于复杂繁琐，本文提出一种简化电路分析方法，可以不用复杂的化简和计算就可以得出LDO的零极点位置分布，并通过几种LDO频率补偿方式为例介绍该方法的应用，最后通过仿真验证了此方法的准确性。

　　引言

　　对于全片内LDO而言，由于没有片外大电容，故很大程度上LDO的稳定性成为全片内LDO设计的难点。而频率特性是衡量稳定性的重要指标，只有清楚电路的零极点的位置分布，才可以对LDO的稳定性进行补偿，最常见的方法就是通过建立小信号模型，利用KCL和KVL等定理对各个方程式进行化简，得出系统传输函数，但这种方法需要的计算量比较大，随着补偿电容和级数的增加，计算会越来越繁琐，不利于快速分析。本文的工作主要是提出一种通过利用简化框图的结构，该结构在分析极点和零点时各采用不同假设从而得到不同的电流通路，可以快速分析出LDO系统零极点的分布情况，最后并通过仿真验证了该方法的可靠性。

　　传统的小信号分析方法

　　如图1所示，普通无片外电容LDO结构一般由误差放大器(EA)，调整管MP以及电阻反馈网络RF1、RF2组成，CL是一个容值很小的电容，对于片内集成的LDO来说，一般只有1pF~50pF左右。以密勒补偿为例，采用传统的小信号分析方法，如图2。　　

 

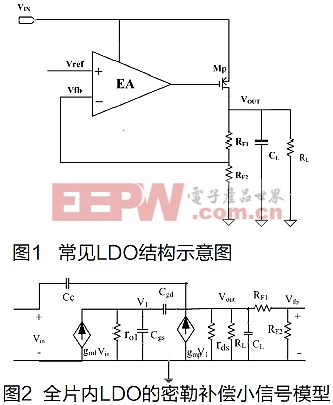
　　其中个g_m1和r_o1分别为误差放大器的跨导和输出电阻，g_mp和r_ds分别为调整管的跨导和沟道电阻，C_gs和C_gd分别为调整管的栅源电容和栅漏电容，C_c为密勒补偿电容。根据KVL和KCL定理可得如下关系：