容差模拟电路的软故障诊断的小波方法

　　0 引言

　　自20世纪70年代以来，模拟电路故障诊断领域已经取得了一定的研究成果，近年来，基于神经网络技术的现代模拟电路软故障诊断方法已成为新的研究热点，神经网络的泛化能力和非线性映射能力，使之能够适用于解决模拟电路故障诊断中的容差和非线性问题，但在软故障实际检测中，由于不同的分类故障之间又不可避免地存在着模糊性，即不同的分类故障可能有相同或相近的故障特征向量，而这仅仅靠神经网络的泛化能力是无法解决的。而量子神经网络被认为是一种具有固有模糊性的网络，它的隐层单元采用多量子能级变换函数，每个多能级变换函数是一系列具有量子间隔偏移的S型函数之和，能将决策的不确定性数据合理地分配到各类故障中，从而减少故障识别的不确定度，提高模式识别的准确性。

　　文章提出了容差模拟电路软故障诊断的小波与量子神经网络方法，利用MonteCarlo分析解决电路容差问题，又利用小波分析，取其能反映故障信号特征的成分做为电路故障特征，再输入给量子神经网络。不仅解决了一个可测试点问题，并提高了辨识故障类别的能力，而且在网络训练之前，利用主元分析降低了网络输入维数。通过实验可以看出，这种方法不仅能实现模拟电路单软软故障诊断，也能实现多软软故障诊断，实验统计结果表明：故障诊断率为100%。

　　1 主元分析

　　主元分析即主成份分析(Principal Component Analysis，简称PCA)，它是最古老的多元统计分析技术之一。主成份分析方法可以将数据从高维数据空间变换到低维特征空间，因而可以用于数据的特征提取及压缩等方面。其实质是将研究对象的多个相关变量转化为少数几个不相关变量的一种多元统计方法。它基于Karhunen-Loeve分解，目的是在数据空间中找一组向量尽可能的解释数据的方差，通过一个特殊的向量矩阵，将数据从原来的高维空间映射到一个低维向量空间，降维后保存了数据的主要信息，从而使数据更易于处理。

　　2 小波分析

　　小波变换的含义是：把一称为基本小波的函数ψ(t)做位移τ后，再在不同尺度α下与待分析信号χ(t)做内积

3 量子神经网络

　　N.B.Karayiannis等人1997年提出多层激励函数的量子神经网络，这种量子神经网络是3层的网状结构，输入层、隐层、输出层，其中输入层和输出层与传统神经网络无异，而隐层的量子神经元借鉴了量子理论中量子态叠加的思想，采用多量子能级变换函数，每个多能级函数是一系列具有量子间隔(Quantum Interval)偏移的ns，个Sigmoid函数的线性叠加，称之为多层激励函数。即隐层神经元的输出可写为

为量子跃迁位置，而量子间隔取决于跃迁位置。量子神经网络的学习分两步，一是对权值的调整，使输人数据对应到不同的类空间中，二是对隐层的量子神经元的量子间隔进行调整，体现数据的不确定性。

　　4 基于小波和量子神经网络的故障诊断原理

　　采用小波与量子神经网络对模拟电路进行软故障诊断的过程，与小波神经网络对模拟电路进行软故障的过程相似：首先将电路的各种故障状态及正常态对应的理论值用PSpice仿真求出，然后用小波变换从输出采样信号中提取故障特征并对特征向量进行归一化;最后是状态识别和故障诊断。其结构如图1所示：

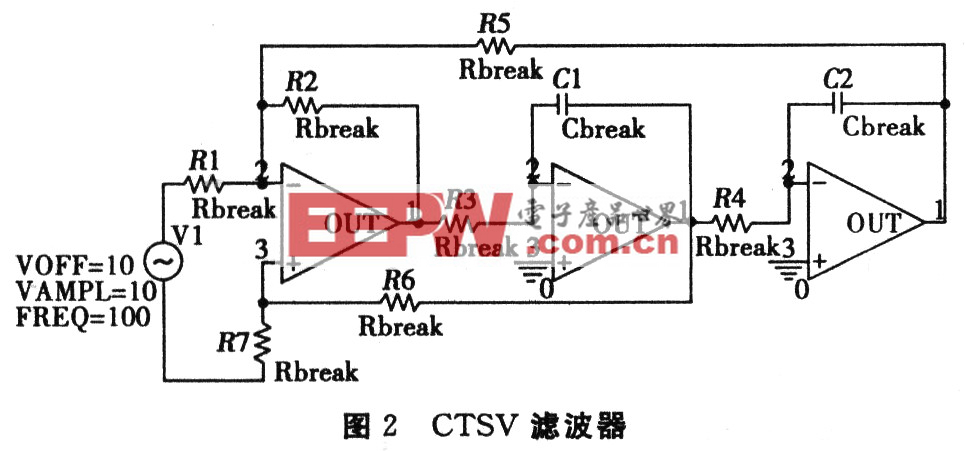
　　诊断过程：

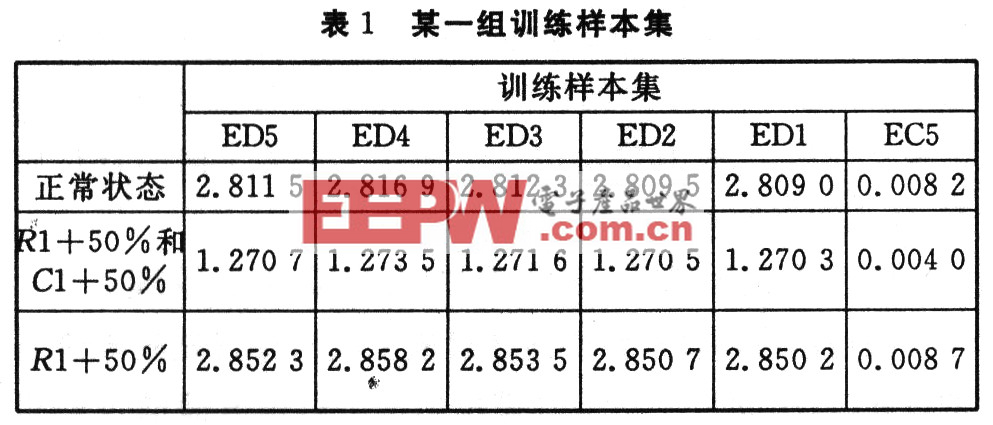
　　(1)构造特征向量，提取能量特征信息：在pspice中对电路的每一种状态进行瞬时分析，取500个采样点，并对每一种故障模式进行300次 MonteCarlo分析，在Probe窗口中选择菜单Viewoutput File，或直接在Probe内选择菜单FileExport将波形采样数据存盘，可得到out节点的具体信息，将数据转化为MATLAB数据文件，然后进行小波分析，在实验中，经分析与比较，小波选择db2小波，对每个故障信号进行5尺度小波分解。得能量特征信息F=(ED5，ED4，…，ED1， EC5)。这里可利用MATLAB中的sumsqr函数。从而得到网络的训练样本集和测试样本集。300次MonteCarlo分析，其中200次为训练样本，100次为测试样本。

　　(2)对测得的数据进行处理：在把小波分解系数序列能量输入给神经网络之前，为了加快网络收敛，有必要对数据进行归一化处理，这里利用MATLAB中的premnmx进行归一化。

　　(3)确定量子与BP神经网络结构和参数：利用文献[3]中算法建立量子神经网络。在实验中，网络的输入节点数为小波分解系数序列能量个数，BP与QNN 均为6，QNN与自适应BP网络均为3个输出节点。隐层的选取及其它由设计者凭经验和试验次数自行决定。本文经过多次试验，确定QNN与BP的隐层节点均为(15，15)，QNN及BP的S型函数的斜率因子均设置为1.0，初始权值取为(-1，1)之间的随机数，期望误差为0.01，初始学习速率为0. 001，动量因子MC为0.90，QNN的隐层采用具有38个量子能级的量子神经元。在训练之前，利用主元分析降低网络输入维数，主元分析在MATLAB 里用princomp函数。

　　(4)训练QNN网络：自适应BP神经网络在第2040步收敛如图3，量子神经网络在第4810步收敛如图4。

　　(5)测试神经网络：为了检验已经训练过的QNN网络与BP网络的性能，现用测试样本(测试样本数据在输入给神经网络之前也进行归一化处理)对网络进行测试，将测试样本，输入到已训练好的BP神经网络、QNN神经网络，从统计结果可以看出，BP的平均诊断率为66.67%，而QNN的平均诊断率为 100%，QNN与BP相比，故障诊断率提高较多。

　　从试验可以看出：BP网络对正常状态和R1+50%无法区分，而QNN对三个状态都能正确区分，QNN网络能够对BP网络无法分类的数据进行正确分类，比如说这两组数据(2.811 3 2.816 8 2.812 1 2.809 3 2.808 9 0.008 2)，(2.852 0 2.857 9 2.853 2 2.850 4 2.850 0 0.008 7)，在实验中，可以观察到：QNN与BP在输入、输出、隐层相同的情况下，增加QNN的隐层神经元的量子能级能提高故障诊断率，与BP隐层神经元相似， QNN隐层神经元的量子能级在增加到某值后继续增加故障诊断率反而减少，隐层神经元的量子能级在增加的同时也降低了网络收敛速度。

　　6 结论

　　提出了基于Pspice、主元分析、小波分析与量子神经网络的模拟电路软故障诊断。例题将QNN网络与BP神经网络的相比，QNN克服了BP网络在模糊分类方面的局限性诊断率为100%。